บทคัดย่อ

ในระบบข้อมูลแบบสุ่ม ส่วนประกอบความถี่ที่มากกว่าครึ่งหนึ่งของอัตราการสุ่มจะ "alias" (เลื่อน) เข้าไปในย่านความถี่ที่สนใจ ส่วนใหญ่แล้ว การ aliasing เป็นผลข้างเคียงที่ไม่พึงประสงค์ ดังนั้นความถี่สูงที่ "undersampled" จึงถูกกรองออกก่อนขั้นตอนอนาล็อกเป็นดิจิทัล (AD) แต่บางครั้ง การ undersampling ก็เป็นไปโดยเจตนา และการ aliasing ทำให้ระบบ AD ทำงานเป็นมิกเซอร์

เอกสารการใช้งานนี้กล่าวถึงข้อกำหนดการกรองที่แตกต่างกันสำหรับระบบข้อมูลแบบสุ่ม โดยอธิบายถึง aliasing และประเภทของตัวกรองที่สามารถใช้สำหรับการป้องกัน aliasing

การกรองเป็นกระบวนการที่พบบ่อยมากจนเรามักจะมองข้ามไป เมื่อเราโทรศัพท์มือถือ ผู้รับจะกรองช่องสัญญาณอื่น ๆ ทั้งหมดออกไป เพื่อให้เราได้รับเฉพาะช่องสัญญาณเฉพาะของเราเท่านั้น เมื่อเราปรับอีควอไลเซอร์บนระบบสเตอริโอ เรากำลังเพิ่มหรือลดสัญญาณเสียงในย่านความถี่เฉพาะอย่างเลือกสรร โดยใช้ตัวกรองแบบแบนด์พาส

ตัวกรองมีบทบาทสำคัญในระบบข้อมูลแบบสุ่มเกือบทั้งหมด ตัวแปลงอนาล็อกเป็นดิจิทัล (ADC) ส่วนใหญ่จะมีตัวกรองนำหน้าเพื่อกำจัดส่วนประกอบความถี่ที่อยู่นอกช่วงของ ADC ADC บางตัวมีการกรองโดยธรรมชาติในโครงสร้างของมัน

มาดูระบบข้อมูลแบบสุ่ม ข้อกำหนดการกรอง และความสัมพันธ์กับการ aliasing กัน

พื้นหลัง

ส่วนประกอบความถี่สูงสุดที่ระบบข้อมูลแบบสุ่มสามารถจัดการได้อย่างแม่นยำคือขีดจำกัด Nyquist อัตราการสุ่มต้องมากกว่าหรือเท่ากับสองเท่าของส่วนประกอบความถี่สูงสุดในสัญญาณอินพุต เมื่อกฎนี้ถูกละเมิด สัญญาณที่ไม่ต้องการหรือไม่พึงประสงค์จะปรากฏในย่านความถี่ที่สนใจ สิ่งนี้เรียกว่า "aliasing"

ตัวอย่างเช่น ในการแปลงสัญญาณ 1kHz เป็นดิจิทัล ต้องใช้อัตราการสุ่มขั้นต่ำ 2kHz ในทางปฏิบัติจริง การสุ่มมักจะสูงกว่าเพื่อเพิ่มระยะขอบและทำให้ข้อกำหนดการกรองมีความสำคัญน้อยลง

เพื่อช่วยให้เข้าใจระบบข้อมูลแบบสุ่มและการ aliasing เราจะดูตัวอย่างภาพยนตร์คลาสสิก

ในภาพยนตร์คาวบอยเก่า ๆ เมื่อรถม้าเร่งความเร็ว ล้อจะหมุนเร็วขึ้นตามที่คาดไว้ จากนั้นล้อดูเหมือนจะช้าลง แล้วหยุด เมื่อรถม้าเร่งความเร็วต่อไป ล้อดูเหมือนจะหมุนย้อนกลับ! ในความเป็นจริง เรารู้ว่าล้อไม่ได้หมุนย้อนกลับ เพราะการกระทำอื่น ๆ ในภาพยนตร์ยังคงดำเนินต่อไป อะไรคือสาเหตุของปรากฏการณ์นี้? คำตอบคืออัตราเฟรมไม่สูงพอที่จะจับภาพการหมุนของล้อได้อย่างแม่นยำ

เพื่อช่วยให้เข้าใจเรื่องนี้ สมมติว่ามีเครื่องหมายที่มองเห็นได้วางอยู่บนล้อรถม้าและล้อถูกหมุน จากนั้นเราจะถ่ายภาพในช่วงเวลาหนึ่ง (หรือตัวอย่าง) เนื่องจากกล้องถ่ายภาพยนตร์จับภาพการเคลื่อนไหวโดยการถ่ายภาพจำนวนหนึ่งต่อวินาที จึงเป็นระบบข้อมูลแบบสุ่มโดยธรรมชาติ เช่นเดียวกับที่ฟิล์มถ่ายภาพล้อเป็นภาพที่ไม่ต่อเนื่อง ADC จะถ่ายภาพสัญญาณไฟฟ้าที่เคลื่อนที่อย่างต่อเนื่อง

เมื่อรถม้าเริ่มเร่งความเร็ว อัตราการสุ่ม (อัตราเฟรมของกล้องถ่ายภาพยนตร์) จะสูงกว่าอัตราการหมุนของล้อมาก ดังนั้นจึงเป็นไปตามเกณฑ์ Nyquist อัตราการสุ่มของกล้องสูงกว่าสองเท่าของอัตราการหมุนของล้อ ดังนั้นจึงสามารถแสดงการเคลื่อนไหวของล้อได้อย่างแม่นยำ และเราเห็นล้อเร่งความเร็วตามที่คาดไว้ (รูปที่ 1a และ 1b)

ที่ขีดจำกัด Nyquist เราจะเห็นสองจุดที่ห่างกัน 180 องศา (รูปที่ 1c) จุดสองจุดนี้โดยทั่วไปไม่สามารถแยกแยะได้จากกันในเวลาด้วยตาของมนุษย์ พวกมันปรากฏพร้อมกันและล้อดูเหมือนจะหยุด ที่ความเร็วล้อนี้ อัตราการหมุนเป็นที่ทราบ (ขึ้นอยู่กับอัตราการสุ่ม) แต่ไม่สามารถระบุทิศทางการหมุนได้ เมื่อรถม้ายังคงเร่งความเร็ว เกณฑ์ Nyquist จะไม่เป็นไปตามอีกต่อไป และมีสองวิธีที่เป็นไปได้ในการมองเห็นล้อ เราสามารถ "เห็น" ว่ามันหมุนไปข้างหน้าและอีกอันหมุนไปในทิศทางย้อนกลับ (รูปที่ 1d)

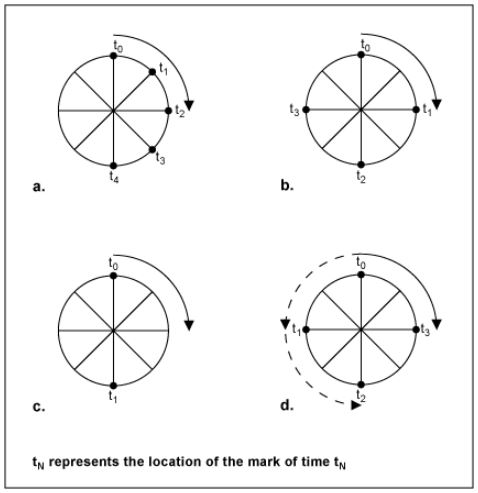
ทั้งสองสามารถมองว่าเป็นทิศทางที่ถูกต้อง ขึ้นอยู่กับว่าคุณ 'เห็น' ล้ออย่างไร แต่ตอนนี้เรามีสัญญาณ aliased นั่นคือมีองค์ประกอบความถี่ในระบบของเราที่ไม่ต้องการและเราไม่สามารถแยกแยะออกจากค่าจริงได้ ทั้งข้อมูลการเคลื่อนที่ไปข้างหน้าและย้อนกลับมีอยู่ เรามักจะเห็นองค์ประกอบย้อนกลับหรือ "sub-multiple" หรือ "image" ขององค์ประกอบไปข้างหน้า เนื่องจากองค์ประกอบไปข้างหน้าหลักจะสังเกตเห็นได้ยากเนื่องจากวิธีการที่การรวมกันของตา/สมองประมวลผลข้อมูล ข้อสังเกตที่น่าสนใจอีกประการหนึ่งคือ ณ จุดที่อัตราการสุ่มตัวอย่างเท่ากับอัตราการหมุนของล้อพอดี ข้อมูลที่ได้จะให้ข้อมูลที่เป็นประโยชน์น้อยมากเนื่องจากเครื่องหมายจะปรากฏที่จุดเดียวกันบนล้อเสมอ ในกรณีนี้เราไม่สามารถบอกได้ว่าล้อกำลังหมุนหรือหยุดนิ่ง

ตอนนี้เข้าสู่ขอบเขตทางคณิตศาสตร์ สมมติว่าล้อเป็นวงกลมหน่วยที่มีพิกัดไซน์และโคไซน์ หากสุ่มตัวอย่างที่จุดสูงสุดบวกและลบของค่าโคไซน์ (ซึ่งมีเฟสต่างกัน 180 องศา) เกณฑ์ Nyquist จะเป็นไปตามข้อกำหนดและค่าโคไซน์ดั้งเดิมสามารถสร้างขึ้นใหม่ได้จากจุดข้อมูลที่สุ่มตัวอย่างสองจุด ดังนั้นขีดจำกัด Nyquist จึงจำเป็นในการสร้างสัญญาณดั้งเดิมขึ้นใหม่ เมื่อมีการเพิ่มจุดมากขึ้นเรื่อยๆ ความสามารถในการจำลองสัญญาณดั้งเดิมก็จะดีขึ้น

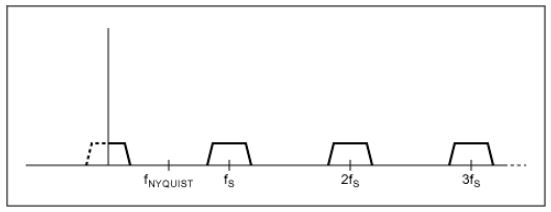
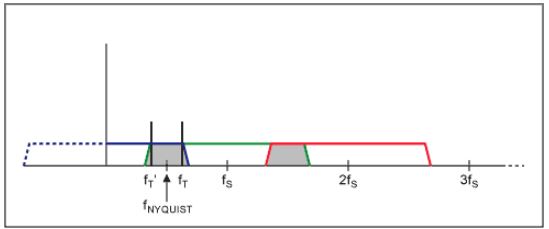
เมื่อย้ายไปยังโดเมนความถี่ รูปที่ 2 แสดงการตอบสนองความถี่ของระบบข้อมูลที่สุ่มตัวอย่าง สังเกตว่าข้อมูลถูกทำซ้ำที่พหุคูณของอัตราการสุ่มตัวอย่าง (สิ่งเหล่านี้คือ 'ภาพ' ของสัญญาณดั้งเดิม) นี่คือลักษณะพื้นฐานของระบบข้อมูลที่สุ่มตัวอย่าง ในรูปที่ 2a เกณฑ์ Nyquist เป็นไปตามข้อกำหนดและไม่มีการเกิด aliasing ในย่านความถี่ที่สนใจ อย่างไรก็ตาม ในรูปที่ 2b สังเกตว่าเกณฑ์ Nyquist ไม่เป็นไปตามข้อกำหนดเนื่องจากความถี่สูงสุดในย่านความถี่ที่สนใจมากกว่าครึ่งหนึ่งของอัตราการสุ่มตัวอย่าง บริเวณที่ทับซ้อนกันคือบริเวณที่เกิด aliasing สัญญาณที่ความถี่ fT ก็ปรากฏที่ fT' คล้ายกับตัวอย่าง aliasing ที่ใช้ล้อเกวียน

อันเดอร์แซมปลิง

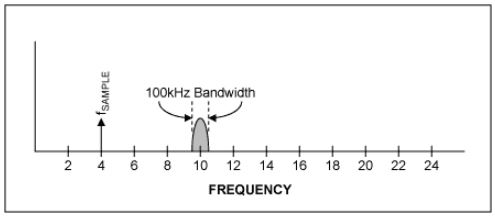
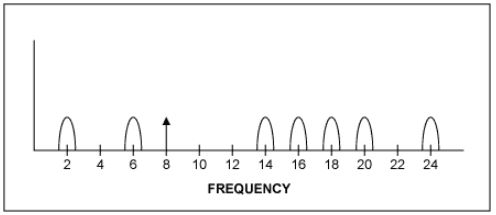
อันเดอร์แซมปลิง เป็นเครื่องมือที่มีประสิทธิภาพที่สามารถนำมาใช้ได้อย่างมีประสิทธิภาพในการใช้งานที่เลือกไว้ ช่วยให้ ADC ทำงานเหมือนมิกเซอร์ได้ โดยสามารถรับสัญญาณพาหะความถี่สูงที่ถูกมอดูเลตและสร้างภาพที่มีความถี่ต่ำกว่าได้ ด้วยวิธีนี้จึงทำงานเหมือนดาวน์คอนเวอร์เตอร์ ข้อดีที่สำคัญอีกประการหนึ่งคือช่วยให้สามารถใช้ ADC ที่มีอัตราการสุ่มตัวอย่างต่ำกว่า Nyquist ซึ่งมักจะมีข้อได้เปรียบด้านต้นทุนอย่างมาก ตัวอย่างเช่น สมมติว่าเรามีพาหะที่ถูกมอดูเลต 10MHz ที่มีแบนด์วิดท์ 100kHz (±50kHz ที่ศูนย์กลาง 10MHz) การ Undersampling ที่ 4MHz จะให้เทอมผลรวมและผลต่างอันดับหนึ่ง (f1 + f2 และ f1 − f2) ที่ 14MHz และ 6MHz และเทอมอันดับสอง (2f1, 2f2, 2f1 + f2, f1 + 2f2, | 2f1 − f2 |, | f1 − 2f2) | ที่ 8MHz, 20MHz, 18MHz, 2MHz, 24MHz และ 16MHz สัญญาณภาพที่ปรากฏที่ 2MHz คือสัญญาณที่น่าสนใจ สังเกตว่าเราได้นำสัญญาณที่ 10MHz และโดยการแปลงเป็นดิจิทัลได้สร้าง alias ที่ 2MHz ตอนนี้เราสามารถทำการประมวลผลสัญญาณในโดเมนดิจิทัล (การกรองและการผสม) เพื่อกู้คืนสัญญาณ 50kHz ดั้งเดิมได้ วิธีการนี้ช่วยลดความจำเป็นในการประมวลผลแบบอนาล็อกที่ซับซ้อน ซึ่งเป็นข้อดีที่สำคัญอย่างหนึ่ง เนื่องจากทุกอย่างทำในโดเมนดิจิทัล หากต้องการเปลี่ยนแปลงประสิทธิภาพและลักษณะของวงจร ก็เพียงแค่แก้ไขซอฟต์แวร์เท่านั้น ในทางตรงกันข้าม สำหรับการออกแบบแบบอนาล็อก ส่วนประกอบฮาร์ดแวร์ของวงจรและการจัดวางอาจต้องเปลี่ยนแปลงเพื่อปรับปรุงประสิทธิภาพของวงจร และสิ่งนี้อาจมีค่าใช้จ่ายสูงมาก

ข้อเสียอย่างหนึ่งของการ Undersampling คือสัญญาณที่ไม่ต้องการสามารถปรากฏในย่านความถี่ที่ต้องการและคุณไม่สามารถแยกแยะออกจากสัญญาณที่ต้องการได้ นอกจากนี้ เมื่อ Undersampling ช่วงความถี่ที่อินพุต ADC มักจะกว้างมาก ในตัวอย่างข้างต้น แม้ว่าอัตราการสุ่มตัวอย่างของเราคือ 4MHz,"""ADC front-end ยังคงต้องรับสัญญาณ 10MHz ในทางตรงกันข้าม หากใช้ตัวผสมสัญญาณอนาล็อกหน้า ADC เพื่อเลื่อนสัญญาณพาหะที่ถูกมอดูเลตลงมาที่เบสแบนด์ แบนด์วิดท์อินพุตของ ADC จะต้องเป็นเพียง 50kHz แทนที่จะเป็น 4MHz ซึ่งช่วยลดความต้องการของ ADC front-end และการกรองอินพุต

การสุ่มตัวอย่างเกิน

การสุ่มตัวอย่างเกิน (Oversampling) ให้สิ่งที่เรียกว่า processing gain เมื่อคุณสุ่มตัวอย่างเกิน คุณจะสุ่มตัวอย่างมากขึ้นด้วยความถี่การสุ่มตัวอย่างที่สูงกว่าที่จำเป็น จากนั้นกรองข้อมูล ซึ่งช่วยลดระดับสัญญาณรบกวนของระบบได้อย่างมีประสิทธิภาพ (เราสมมติว่าสัญญาณรบกวนของเราเป็นสัญญาณรบกวนสีขาวแบบบรอดแบนด์) ซึ่งแตกต่างจากการเฉลี่ย ซึ่งมีการสุ่มตัวอย่างจำนวนมากและสัญญาณรบกวนจะถูกเฉลี่ย การสุ่มตัวอย่างเกินสามารถคิดได้ในลักษณะนี้: หากสัญญาณอินพุตมาจากแหล่งสัญญาณที่กวาดความถี่อินพุต สเปกตรัมความถี่สามารถแบ่งออกเป็นช่วงหรือ "bin" โดยแต่ละ bin มีความกว้างคงที่ สัญญาณรบกวนบรอดแบนด์จะกระจายไปทั่วช่วงความถี่ที่สนใจทั้งหมด ดังนั้นแต่ละ bin จึงมีสัญญาณรบกวนจำนวนหนึ่ง ตอนนี้หากอัตราการสุ่มตัวอย่างเพิ่มขึ้น จำนวน bin ความถี่ก็จะเพิ่มขึ้นด้วย ในกรณีนี้ สัญญาณรบกวนจำนวนเท่าเดิมยังคงอยู่ แต่เรามี bin มากขึ้นที่จะกระจายออกไป จากนั้นเราใช้ตัวกรองเพื่อกำจัดสัญญาณรบกวนที่อยู่นอกย่านความถี่ที่สนใจ ผลลัพธ์คือแต่ละ bin มีสัญญาณรบกวนน้อยลง และด้วยเหตุนี้เราจึงลดระดับสัญญาณรบกวนของระบบได้อย่างมีประสิทธิภาพโดยการสุ่มตัวอย่างเกิน

ตัวอย่างเช่น หากเรามี ADC 2ksps (เราใช้ขีดจำกัด Nyquist ที่ 1kHz ในสูตรต่อไปนี้) และสัญญาณ 1kHz โดยมีตัวกรองดิจิทัล 1kHz ตามหลัง ADC การประมวลผลจะได้รับโดย: −10 × log (1kHz/1kHz) = 0dB หากเราเพิ่มอัตราการสุ่มตัวอย่างเป็น 10ksps processing gain จะเป็น −10 × log (1kHz/5kHz) = 7dB หรือประมาณ 1 บิตของความละเอียด (1 บิตประมาณเท่ากับ 6dB ของการปรับปรุงอัตราส่วนสัญญาณต่อสัญญาณรบกวน (SNR)) โดยการสุ่มตัวอย่างเกิน สัญญาณรบกวนไม่ได้ลดลง แต่สัญญาณรบกวนได้กระจายไปทั่วแบนด์วิดท์ที่กว้างขึ้น ทำให้สัญญาณรบกวนบางส่วนอยู่นอกย่านความถี่ที่สนใจ (ด้วยตัวกรองดิจิทัลของเรา) และด้วยเหตุนี้จึงให้ผลว่าสัญญาณรบกวนลดลง การปรับปรุงสัญญาณรบกวนนี้ขึ้นอยู่กับสมการต่อไปนี้:

การปรับปรุง SNR (dB) = 10 × LOGA/B โดยที่ A เท่ากับสัญญาณรบกวน และ B เท่ากับสัญญาณรบกวนที่สุ่มตัวอย่างเกิน

อีกวิธีหนึ่งในการกล่าวคือ การสุ่มตัวอย่างเกินจะลดสัญญาณรบกวนการควอนไทซ์ RMS ในย่านความถี่ลงด้วยรากที่สองของอัตราส่วนการสุ่มตัวอย่างเกิน หรือหากสัญญาณรบกวนลดลงสองเท่า จะมี processing gain ที่มีประสิทธิภาพ 3dB โปรดจำไว้ว่าเรากำลังพูดถึงสัญญาณรบกวนบรอดแบนด์เท่านั้น แหล่งสัญญาณรบกวนอื่น ๆ และข้อผิดพลาดอื่น ๆ ไม่สามารถกำจัดได้ง่ายๆ ด้วยการสุ่มตัวอย่างเกิน

ตัวกรองป้องกันการซ้อนทับ

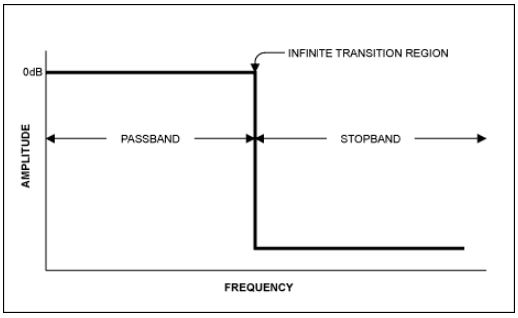
ด้วยพื้นฐานนี้ เราจะมาดูตัวกรองป้องกันการซ้อนทับ (Anti-Alias Filters) เมื่อเลือกตัวกรอง เป้าหมายคือการให้ความถี่คัตออฟที่กำจัดสัญญาณที่ไม่ต้องการออกจากอินพุต ADC หรืออย่างน้อยก็ลดทอนสัญญาณเหล่านั้นจนถึงจุดที่ไม่ส่งผลเสียต่อวงจร ตัวกรองป้องกันการซ้อนทับเป็นตัวกรองความถี่ต่ำที่ทำหน้าที่นี้ แล้วจะเลือกตัวกรองที่เหมาะสมได้อย่างไร พารามิเตอร์สำคัญที่ต้องสังเกตคือปริมาณการลดทอน (หรือริปเปิล) ในย่านความถี่ผ่าน การลดทอนของตัวกรองที่ต้องการในย่านความถี่หยุด ความชันในบริเวณการเปลี่ยนผ่าน และความสัมพันธ์ของเฟสของความถี่ต่างๆ เมื่อผ่านตัวกรอง (รูปที่ 4a)

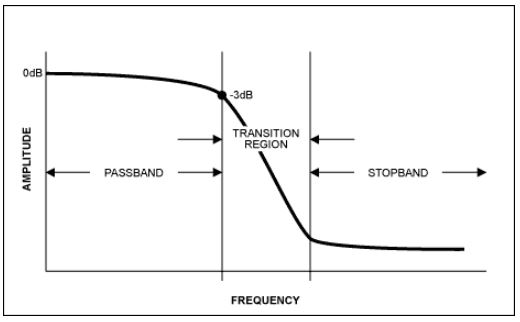
ตัวกรองในอุดมคติมีการตอบสนองแบบ "กำแพงอิฐ" (รูปที่ 4b) นั่นคือ มีอัตราส่วนการเปลี่ยนผ่านที่ไม่มีที่สิ้นสุด อย่างไรก็ตาม สิ่งนี้ไม่เคยเกิดขึ้นในแอปพลิเคชันจริง ยิ่งการลดทอนชันเท่าใด 'Q' หรือปัจจัยคุณภาพของตัวกรองก็จะยิ่งสูงขึ้น และยิ่ง Q สูงเท่าใด การออกแบบตัวกรองก็จะยิ่งซับซ้อนมากขึ้นเท่านั้น Q ที่สูงอาจนำไปสู่ความไม่เสถียรของตัวกรองและการสั่นด้วยตัวเองที่ความถี่มุมที่ต้องการหัวใจสำคัญในการเลือกฟิลเตอร์คือการทราบความถี่และแอมพลิจูดที่สอดคล้องกันของสัญญาณรบกวน ตัวอย่างเช่น ในโทรศัพท์มือถือ ผู้ออกแบบจะทราบแอมพลิจูดและตำแหน่งที่แย่ที่สุดของสัญญาณข้างเคียง และออกแบบตามนั้น สัญญาณบางอย่างไม่สามารถคาดการณ์ได้ในโดเมนความถี่ และแม้แต่สัญญาณรบกวนที่ทราบแล้วบางส่วนก็มีขนาดใหญ่เกินกว่าที่จะลดทอนได้อย่างเพียงพอ แต่จากสภาพแวดล้อมและการใช้งาน คุณสามารถพิจารณาการรบกวนที่ทราบแล้วและออกแบบเพื่อลดผลกระทบของการรบกวนแบบสุ่มเพื่อให้การทำงานมีความทนทานมากขึ้น

เมื่อทราบความถี่สัญญาณที่สนใจแล้ว ให้ใช้โปรแกรมฟิลเตอร์อย่างง่ายเพื่อกำหนดโครงสร้างฟิลเตอร์ที่จำเป็นเพื่อให้เป็นไปตามข้อกำหนดของย่านความถี่ผ่าน ย่านความถี่หยุด และย่านการเปลี่ยนผ่าน ในบรรดาฟิลเตอร์พื้นฐานสี่ประเภท แต่ละประเภทมีข้อดีของตัวเอง (รูปที่ 5)

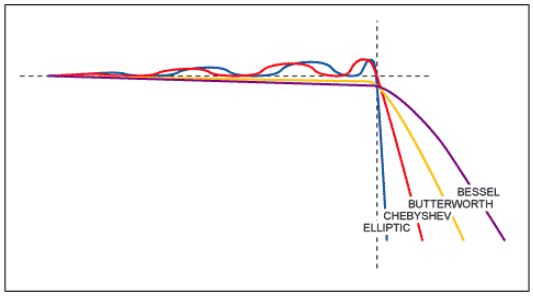
ตัวอย่างเช่น ฟิลเตอร์ Butterworth มีย่านความถี่ผ่านที่ราบเรียบที่สุด ซึ่งหมายความว่ามีการลดทอนน้อยที่สุดในช่วงความถี่ที่ต้องการ ฟิลเตอร์ Bessel มีการลดลงอย่างค่อยเป็นค่อยไป แต่ข้อได้เปรียบหลักคือมีคุณสมบัติเฟสเชิงเส้น ซึ่งหมายความว่าส่วนประกอบความถี่แต่ละส่วนจะถูกหน่วงเวลาเท่ากันเมื่อผ่านฟิลเตอร์ คุณสมบัติเฟสเชิงเส้นมักถูกระบุว่าเป็นความล่าช้าของกลุ่มคงที่ เนื่องจากความล่าช้าของกลุ่มถูกกำหนดให้เป็นอนุพันธ์ของคุณสมบัติเฟสเทียบกับความถี่ ฟิลเตอร์ Chebyshev มีการลดลงที่ชันกว่า แต่มีริปเปิลในย่านความถี่ผ่านมากกว่า ฟิลเตอร์ Elliptic มีการลดลงที่ชันที่สุด สำหรับฟิลเตอร์ป้องกันการซ้อนทับอย่างง่าย ฟิลเตอร์ RC แบบพาสซีฟขั้วเดียวอย่างง่ายมักเป็นที่ยอมรับ ในกรณีอื่นๆ ฟิลเตอร์แอคทีฟ (เช่น ใช้ op amp) ทำงานได้ดี ข้อดีอย่างหนึ่งของฟิลเตอร์แอคทีฟคือสำหรับฟิลเตอร์หลายลำดับ การทำงานของฟิลเตอร์จะไวต่อค่าของส่วนประกอบภายนอกน้อยลง โดยเฉพาะอย่างยิ่งค่า 'Q' ของฟิลเตอร์

ฟิลเตอร์ป้องกันการซ้อนทับโดยทั่วไปไม่จำเป็นต้องแม่นยำเกี่ยวกับตำแหน่งของความถี่มุม ดังนั้นจึงมีช่องว่างในการออกแบบ ตัวอย่างเช่น หากคุณต้องการความราบเรียบสูงสุด แต่ยังมีการลดทอนมากเกินไปในย่านความถี่ผ่าน การเลื่อนความถี่มุมออกไปอีกอาจแก้ปัญหาได้ หากการลดทอนย่านความถี่หยุดต่ำเกินไป ให้เพิ่มจำนวนขั้วในฟิลเตอร์ อีกวิธีหนึ่งคือการขยายสัญญาณหลังจากกรองเพื่อเพิ่มขนาดของสัญญาณเมื่อเทียบกับขนาดของสัญญาณที่ไม่ต้องการ