หากผลการทดลองของคุณไม่ตรงกับค่าในตำราเรียน ก็ไม่ใช่ความผิดของคุณเสมอไป ข้อผิดพลาดในการวัดบางอย่างเป็นสิ่งที่หลีกเลี่ยงไม่ได้ เมื่อคุณเข้าใจประเภทต่างๆ ของข้อผิดพลาดแล้ว ผลการทดลองของคุณก็จะเริ่มมีความหมายมากขึ้นในที่สุด

ในบทความนี้ คุณจะได้เรียนรู้ว่าข้อผิดพลาดในการวัดคืออะไร ประเภทต่างๆ พร้อมตัวอย่าง วิธีลดข้อผิดพลาด และวิธีการคำนวณข้อผิดพลาดอย่างถูกต้อง

ข้อผิดพลาดในการวัดคืออะไร?

ความคลาดเคลื่อนระหว่างค่าที่วัดได้ของปริมาณหนึ่งกับค่าที่แท้จริง (ค่าที่วัดได้จริง) เรียกว่า ข้อผิดพลาดในการวัด

ค่าที่แท้จริงคือค่าจริงของปริมาณใดๆ ที่ปราศจากข้อผิดพลาดโดยสิ้นเชิง

เนื่องจากข้อผิดพลาดเหล่านี้เกิดขึ้นระหว่างการทดลอง จึงเรียกอีกอย่างว่าข้อผิดพลาดในการทดลอง

กระบวนการตรวจสอบข้อผิดพลาดทั้งหมดที่ส่งผลต่อผลการวัด เรียกว่า การวิเคราะห์ข้อผิดพลาด

ข้อผิดพลาดในการทดลองหรือข้อผิดพลาดในการวัดสามารถส่งผลต่อค่าที่วัดได้สามวิธีที่แตกต่างกัน เราจึงได้จำแนกประเภทของข้อผิดพลาดเหล่านี้ออกเป็นประเภทต่างๆ ดังนี้

ข้อผิดพลาดในการวัดมีกี่ประเภทบ้าง

โดยทั่วไป ข้อผิดพลาดในการวัดมีอยู่ 3 ประเภท

• ข้อผิดพลาดแบบสุ่ม
• ข้อผิดพลาดเชิงระบบ
• ข้อผิดพลาดร้ายแรง

ข้อผิดพลาดแบบสุ่ม

เมื่อคุณวัดปริมาณเดียวกันซ้ำแล้วซ้ำเล่าภายใต้เงื่อนไขเดียวกัน แต่ยังคงได้ผลลัพธ์ที่แตกต่างกันเล็กน้อย ความแปรผันในผลลัพธ์เหล่านี้เกิดจากข้อผิดพลาดที่เรียกว่า ข้อผิดพลาดแบบสุ่ม

เรารู้สาเหตุและแหล่งที่มาของข้อผิดพลาดเหล่านี้ แต่ความแปรผันที่เกิดขึ้นในแต่ละการวัดนั้นไม่สามารถคาดเดาได้อย่างแม่นยำ

ข้อผิดพลาดเหล่านี้เกิดขึ้นเพราะบางสิ่งบางอย่างเปลี่ยนแปลงไปอย่างไม่คาดคิด และเราไม่สามารถควบคุมได้ นั่นเป็นเหตุผลที่เราไม่สามารถกำจัดข้อผิดพลาดเหล่านี้ได้อย่างสมบูรณ์

แหล่งที่มาของข้อผิดพลาดแบบสุ่มในการวัด พร้อมตัวอย่าง

เราจัดการกับข้อผิดพลาดแบบสุ่มด้วยวิธีการทางสถิติ (เช่น การหาค่าเฉลี่ย) แทนที่จะใช้การแบ่งประเภท ดังนั้น การแบ่งประเภทข้อผิดพลาดออกเป็นชนิดต่างๆ จึงไม่มีประโยชน์ เราเพียงแค่ใช้วิธีการทางสถิติเพื่อลดข้อผิดพลาดแบบสุ่มลง

ด้วยเหตุนี้เราจึงกล่าวถึงเฉพาะแหล่งที่มาเท่านั้น

แหล่งที่มาสามประเภทที่แตกต่างกันสามารถทำให้เกิดข้อผิดพลาดแบบสุ่มได้

• แหล่งที่มาด้านสิ่งแวดล้อม
• แหล่งกำเนิดเสียงดนตรี
• แหล่งข้อมูลจากการสังเกตการณ์

แหล่งที่มาด้านสิ่งแวดล้อม

ข้อผิดพลาดแบบสุ่มอาจเกิดขึ้นจากความผันผวนอย่างฉับพลันของสภาพแวดล้อม เช่น อุณหภูมิ ความดัน หรือการสั่นสะเทือน

ตัวอย่างเช่น,

1) ในขณะที่วัดแรงดันไฟฟ้าของแบตเตอรี่ด้วยมัลติมิเตอร์ ความผันผวนเล็กน้อยจากอุปกรณ์ไฟฟ้าใกล้เคียง เช่น พัดลม หลอดไฟฟลูออเรสเซนต์ และเราเตอร์ Wi-Fi อาจสร้างสนามแม่เหล็กไฟฟ้าที่ก่อให้เกิดสัญญาณรบกวนในวงจรของมัลติมิเตอร์ได้

2) กระดาษอาจมีน้ำหนักเพิ่มขึ้นหรือลดลงเล็กน้อยบนตาชั่งเนื่องจากการเปลี่ยนแปลงของความชื้น เพราะกระดาษจะดูดซับหรือสูญเสียน้ำจากอากาศ

3) กระแสลมเล็กน้อยจากพัดลม หน้าต่าง หรือแม้แต่ลมหายใจของคุณ สามารถทำให้ค่าน้ำหนักของวัตถุเบาเปลี่ยนแปลงไปบนเครื่องชั่งดิจิทัลได้ เนื่องจากความเคลื่อนไหวของอากาศเหล่านี้เปลี่ยนแปลงไปอย่างไม่แน่นอน การวัดแต่ละครั้งจึงได้ค่าที่แตกต่างกันเล็กน้อย

แหล่งกำเนิดเสียงดนตรี

ข้อผิดพลาดแบบสุ่มอาจเกิดจากความผันผวนแบบสุ่มภายในเครื่องมือได้เช่นกัน ตัวอย่างเช่น

1) ค่าที่อ่านได้จากมัลติมิเตอร์อาจคลาดเคลื่อนเล็กน้อยเนื่องจากสัญญาณรบกวนทางอิเล็กทรอนิกส์เล็กน้อยภายในตัวเครื่อง

2) ในมิเตอร์แบบอนาล็อก ชิ้นส่วนภายในของเข็ม เช่น ขดลวด สปริง แม่เหล็ก และลูกปืน มีความไม่สมบูรณ์ตามธรรมชาติเล็กน้อยและการเคลื่อนไหวขนาดเล็กที่ทำให้เข็มสั่นไหวอย่างคาดเดาไม่ได้

การเปลี่ยนแปลงภายในเล็กๆ เหล่านี้เกิดขึ้นเอง แม้ว่าค่าที่วัดได้จะคงที่ก็ตาม

3) เมื่อวัดความเข้มแสงคงที่ ผลลัพธ์จะผันผวนเล็กน้อย

ปรากฏการณ์นี้เกิดขึ้นเนื่องจากโฟโตไดโอดภายในเซ็นเซอร์รับโฟตอนในลักษณะสุ่มตามธรรมชาติ บางครั้งอาจมีโฟตอนเข้ามามากกว่าปกติ บางครั้งอาจมีน้อยกว่าปกติ และความสุ่มนี้เองที่ก่อให้เกิดสัญญาณรบกวนแบบช็อตนอยส์

วงจรอิเล็กทรอนิกส์ของเซ็นเซอร์ยังเพิ่มความแปรผันเล็กๆ น้อยๆ เข้าไปอีก ดังนั้นเมื่อรวมกันแล้วจึงทำให้เกิดการเปลี่ยนแปลงเล็กๆ น้อยๆ ที่คาดเดาไม่ได้ในผลลัพธ์

แหล่งข้อมูลจากการสังเกตการณ์

ความผันแปรเล็กน้อยแบบสุ่มที่เกิดขึ้นเนื่องจากความไม่สมบูรณ์แบบของผู้ทำการทดลอง เช่น การสั่นของมือเล็กน้อย การโฟกัสสายตาที่ไม่สม่ำเสมอ และความแปรปรวนของเวลาตอบสนอง

ตัวอย่างของข้อผิดพลาดแบบสุ่มที่เกิดจากแหล่งข้อมูลการสังเกต ได้แก่:

1) เมื่อคุณวัดเวลาของการแกว่ง ปฏิกิริยาของคุณในการเริ่มหรือหยุดนาฬิกาจับเวลาอาจเปลี่ยนแปลงเล็กน้อยในแต่ละครั้ง ส่งผลให้เวลาที่บันทึกไว้แต่ละครั้งแตกต่างจากค่าที่แท้จริงเล็กน้อย

2) เมื่อคุณขึ้นไปยืนบนตาชั่ง การเปลี่ยนแปลงเล็กน้อยในท่าทาง ตำแหน่งเท้า หรือการทรงตัวจะเกิดขึ้นทุกครั้ง ส่งผลให้ค่าของน้ำหนักแตกต่างกันเล็กน้อย

ความผันแปรเหล่านี้ไม่มีทิศทางที่แน่นอน บางครั้งค่าที่วัดได้อาจสูงกว่าเล็กน้อย บางครั้งอาจต่ำกว่าเล็กน้อย

3) เมื่อวัดความยาวของดินสอ สายตาของคุณอาจคลาดเคลื่อนเล็กน้อยในแต่ละครั้ง ทำให้เกิดความคลาดเคลื่อนเล็กน้อยที่ไม่สามารถคาดเดาได้ในการวัด

วิธีลดข้อผิดพลาดแบบสุ่ม

วิธีที่พบได้บ่อยและมีประสิทธิภาพที่สุดในการลดข้อผิดพลาดแบบสุ่มคือการวัดหลายครั้งแล้วคำนวณค่าเฉลี่ย

ในแต่ละครั้งที่คุณทำการวัด ค่าที่ได้อาจสูงกว่าหรือต่ำกว่าค่าจริงเล็กน้อย เนื่องจากการเปลี่ยนแปลงเล็กน้อยที่ไม่สามารถคาดเดาได้

โดยการวัดหลายๆ ครั้ง ค่าความคลาดเคลื่อนที่สูงกว่าและต่ำกว่าค่าที่แท้จริงจะหักล้างกันเอง และค่าเฉลี่ยจะให้ค่าที่ใกล้เคียงกับค่าที่แท้จริงมากขึ้น

ยิ่งคุณทำการวัดมากเท่าไหร่ ผลกระทบจากข้อผิดพลาดแบบสุ่มก็จะยิ่งน้อยลงเท่านั้น

ข้อผิดพลาดเชิงระบบ

หากคุณทำการวัดปริมาณใดปริมาณหนึ่งหลายครั้งภายใต้เงื่อนไขเดียวกัน และการวัดแต่ละครั้งแสดงค่าที่แตกต่างจากค่าจริงอย่างสม่ำเสมอ ข้อผิดพลาดนั้นเรียกว่าข้อผิดพลาดเชิงระบบ

ข้อผิดพลาดเหล่านี้มีรูปแบบที่คาดเดาได้ เนื่องจากทำให้เกิดการเปลี่ยนแปลงแบบเดียวกันในการวัดทุกครั้ง นอกจากนี้ ผลลัพธ์ที่ได้จะสูงกว่าหรือต่ำกว่าค่าที่แท้จริง

ข้อผิดพลาดที่เป็นระบบอาจเป็นค่าคงที่หรือเป็นสัดส่วนก็ได้

ในการวัดแบบความคลาดเคลื่อนคงที่อย่างเป็นระบบ ความคลาดเคลื่อนจะมีค่าเท่าเดิม ไม่ว่าปริมาณที่วัดจะมีมากหรือน้อยก็ตาม วิธีการนี้ไม่ขึ้นอยู่กับปริมาณที่วัด

ตัวอย่างเช่น หากเครื่องชั่งอ่านค่าได้ 2 กิโลกรัมเมื่อว่างเปล่า แสดงว่ามีค่าความคลาดเคลื่อนเป็นศูนย์ คือ +2 กิโลกรัม นี่คือค่าความคลาดเคลื่อนคงที่ที่เป็นระบบ เนื่องจากค่าความคลาดเคลื่อนจะไม่เพิ่มขึ้นหรือลดลงเมื่อปริมาณเปลี่ยนแปลง

ดังนั้น ถ้าคุณวางของหนัก 3 กิโลกรัมลงบนตาชั่ง มันจะแสดงค่า 5 กิโลกรัม และถ้าคุณวางของหนัก 6 กิโลกรัม มันจะแสดงค่า 8 กิโลกรัม

เนื่องจากค่าความคลาดเคลื่อนเหล่านี้เป็นค่าสัมบูรณ์คงที่ ดังนั้นค่าความคลาดเคลื่อนสัมพัทธ์หรือเปอร์เซ็นต์จะดูมากเมื่อปริมาณตัวอย่างมีน้อย และจะดูน้อยเมื่อปริมาณตัวอย่างมีมาก

ในกรณีของความคลาดเคลื่อนเชิงสัดส่วนอย่างเป็นระบบ ความคลาดเคลื่อนจะเปลี่ยนแปลงไปตามสัดส่วนของปริมาณที่วัด

หมายความว่าเปอร์เซ็นต์ความคลาดเคลื่อนคงที่ แต่ความคลาดเคลื่อนสัมบูรณ์จะเพิ่มขึ้นเมื่อค่าเพิ่มขึ้น และจะลดลงเมื่อค่าลดลง

เพื่อให้เข้าใจง่ายขึ้น ลองนึกภาพว่าคุณกำลังใช้ไม้บรรทัดที่ทำจากเหล็ก ซึ่งได้รับการสอบเทียบที่อุณหภูมิ 15 องศาเซลเซียส

ในช่วงฤดูร้อน เมื่ออุณหภูมิสูงขึ้น ไม้บรรทัดโลหะจะขยายตัวเล็กน้อย ส่งผลให้ขีดบอกระยะแต่ละเซนติเมตรขยับห่างกันเล็กน้อย

หากไม้บรรทัดขยายออกตามสัดส่วน 0.1% ความยาวที่วัดได้ของวัตถุจะน้อยกว่าความยาวจริงเล็กน้อย เนื่องจากช่องแบ่งบนไม้บรรทัดจะพอดีกับวัตถุน้อยลง

• เครื่องมือนี้วัดวัตถุขนาด 10 ซม. ได้ค่า 9.99 ซม. ค่าความคลาดเคลื่อนสัมบูรณ์คือ −0.01 ซม.
• เครื่องมือนี้วัดวัตถุขนาด 50 ซม. ได้เป็น 49.95 ซม. ดังนั้นค่าความคลาดเคลื่อนสัมบูรณ์จึงเท่ากับ -0.05 ซม.
• วัตถุขนาด 100 ซม. จะถูกวัดได้ 99.9 ซม. ค่าความคลาดเคลื่อนสัมบูรณ์ของค่านี้คือ -0.1 ซม.
• เครื่องมือนี้วัดวัตถุขนาด 200 ซม. ได้ค่า 199.8 ซม. โดยค่าที่วัดได้นี้มีค่าความคลาดเคลื่อนสัมบูรณ์เท่ากับ -0.2 ซม.

คุณสามารถวิเคราะห์ได้ว่า เมื่อค่าที่วัดได้เพิ่มขึ้น ค่าความคลาดเคลื่อนสัมบูรณ์ก็จะเพิ่มขึ้นด้วย แต่ค่าความคลาดเคลื่อนสัมพัทธ์หรือค่าความคลาดเคลื่อนเป็นเปอร์เซ็นต์จะยังคงเท่าเดิม คือ 0.1%

ประเภทของข้อผิดพลาดเชิงระบบในการวัด พร้อมตัวอย่าง

การจำแนกประเภทข้อผิดพลาดที่เป็นระบบนั้นมีประโยชน์ เพราะการระบุประเภทจะช่วยให้สามารถแก้ไขหรือปรับเทียบได้

มีแหล่งที่มาหลักสามแหล่งที่สามารถก่อให้เกิดข้อผิดพลาดอย่างเป็นระบบได้ โดยแต่ละประเภทของข้อผิดพลาดจะถูกตั้งชื่อตามแหล่งที่มาที่ทำให้เกิดข้อผิดพลาดนั้น

• ข้อผิดพลาดเชิงระบบด้านสิ่งแวดล้อม
• ข้อผิดพลาดเชิงระบบของเครื่องมือ
• ข้อผิดพลาดเชิงระบบในการสังเกต

ข้อผิดพลาดเชิงระบบด้านสิ่งแวดล้อม

ข้อผิดพลาดเชิงระบบด้านสิ่งแวดล้อม คือ ข้อผิดพลาดที่เกิดขึ้นอย่างสม่ำเสมอในการวัด ซึ่งเป็นผลมาจากปัจจัยด้านสิ่งแวดล้อม เช่น อุณหภูมิ ความชื้น ความดัน หรือสนามไฟฟ้าและสนามแม่เหล็กภายนอก

เนื่องจากผลลัพธ์ที่ได้นั้นเหมือนกันทุกครั้งที่ทำการวัด จึงสามารถคาดการณ์ได้

มาทำความเข้าใจด้วยตัวอย่างกันดีกว่า

1) ไม้บรรทัดจะขยายหรือหดตัวตามอุณหภูมิเนื่องจากการขยายตัวทางความร้อนของวัสดุ

ในฤดูร้อน ขีดบอกระยะบนไม้บรรทัดจะห่างกันมากขึ้นเล็กน้อย ทำให้ความยาวที่วัดได้ดูสั้นกว่าความยาวจริง

ในฤดูหนาว รอยขีดจะอยู่ใกล้กันมากขึ้น ดังนั้นความยาวที่วัดได้จึงดูยาวกว่าความยาวจริง

2) เครื่องชั่งน้ำหนักที่ไวต่อความชื้นจะดูดซับความชื้นในสภาพที่มีความชื้นสูง การวัดแต่ละครั้งจึงได้ค่าที่สูงกว่าค่าจริงเล็กน้อย

ค่าความคลาดเคลื่อนยังคงเท่าเดิมในการวัดแต่ละครั้ง เนื่องจากความชื้นคงที่

3) แอมมิเตอร์ที่วางไว้ใกล้แม่เหล็กแรงสูงจะแสดงค่ากระแสไฟฟ้าสูงกว่าหรือต่ำกว่าค่ากระแสไฟฟ้าจริงเล็กน้อย ข้อผิดพลาดนี้เกิดขึ้นอย่างสม่ำเสมอ ตราบใดที่ยังมีสนามแม่เหล็กอยู่

ข้อผิดพลาดเชิงระบบของเครื่องมือ

ข้อผิดพลาดที่เกิดขึ้นอย่างสม่ำเสมอและคาดการณ์ได้ ซึ่งเกิดจากตัวเครื่องมือวัดเอง เรียกว่า ข้อผิดพลาดเชิงระบบจากเครื่องมือวัด (Instrumental Systematic Error)

เครื่องมืออาจเก่า บำรุงรักษาไม่ดี หรือปรับเทียบไม่ถูกต้อง ซึ่งอาจทำให้ได้ค่าที่อ่านได้ผิดพลาดอย่างต่อเนื่อง

ตัวอย่าง:

1) ข้อผิดพลาดศูนย์ (Zero error) เป็นข้อผิดพลาดที่เป็นระบบซึ่งเกิดจากตัวเครื่องมือเอง เกิดขึ้นเมื่อเครื่องมือไม่แสดงค่าศูนย์แม้ว่าจะไม่มีการวัดสิ่งใดก็ตาม

เนื่องจากจุดเริ่มต้นไม่ถูกต้องอยู่แล้ว เครื่องมือจึงปรับค่าการวัดทุกครั้งไปในปริมาณเท่ากัน

2) หากขีดบอกอุณหภูมิบนเทอร์โมมิเตอร์อยู่ห่างกันมากกว่าที่ควรจะเป็น แสดงว่าแต่ละขีดบอกอุณหภูมิมีช่วงกว้างกว่าที่ตั้งใจไว้

ดังนั้น เมื่อปรอทสูงขึ้นถึงระดับหนึ่ง เทอร์โมมิเตอร์จะอ่านค่าอุณหภูมิได้ต่ำกว่าอุณหภูมิที่แท้จริง

3) สมมติว่าเจ้าหน้าที่ห้องปฏิบัติการไม่ได้ทำความสะอาดเครื่องชั่งเป็นประจำ ฝุ่นละออง คราบไขมัน หรือสนิมจึงสะสมอยู่บนถาดและจุดหมุน

น้ำหนักส่วนเกินนี้ทำให้เครื่องชั่งแสดงค่าสูงกว่าหรือต่ำกว่าน้ำหนักจริงเล็กน้อยอย่างสม่ำเสมอ

ข้อผิดพลาดเชิงระบบในการสังเกต

ข้อผิดพลาดเชิงระบบในการสังเกต คือ ข้อผิดพลาดที่สม่ำเสมอและคาดการณ์ได้ ซึ่งเกิดขึ้นเนื่องจากบุคคลนั้นวัดค่าด้วยวิธีที่ผิดพลาดแบบเดิมซ้ำแล้วซ้ำเล่า

ตัวอย่าง:

1) ข้อผิดพลาดจากพารัลแลกซ์เป็นข้อผิดพลาดเชิงระบบในการสังเกตการณ์

ปรากฏการณ์นี้เกิดขึ้นเมื่อคุณมองดูมาตราส่วนหรือส่วนโค้งของของเหลวจากมุมเอียง ซึ่งทำให้ค่าที่อ่านได้ดูสูงหรือต่ำกว่าความเป็นจริง

ควรจัดระดับสายตาให้ตรงกับตัวบทที่คุณกำลังอ่าน เพื่อหลีกเลี่ยงความคลาดเคลื่อนจากมุมมองที่แตกต่างกัน (parallax error)

2) วางวัตถุผิดตำแหน่งเสมอ (เช่น เริ่มจาก 1 ซม. แทนที่จะเป็น 0 ซม.) การวัดความยาวแต่ละครั้งจะคลาดเคลื่อนไปในปริมาณเท่ากัน

3) เมื่อจับเวลาเหตุการณ์ด้วยนาฬิกาจับเวลา ผู้ทำการทดลองอาจมีความล่าช้าโดยธรรมชาติประมาณ 0.2-0.3 วินาทีในการเริ่ม/หยุด ซึ่งความล่าช้าเล็กน้อยนี้จะทำให้การวัดเวลาทั้งหมดคลาดเคลื่อนไปอย่างสม่ำเสมอ

วิธีการลดข้อผิดพลาดเชิงระบบ

ต่างจากความคลาดเคลื่อนแบบสุ่ม ความคลาดเคลื่อนแบบเป็นระบบไม่สามารถลดลงได้โดยใช้วิธีค่าเฉลี่ย เนื่องจากความคลาดเคลื่อนเกิดขึ้นเพียงทิศทางเดียว

ไม่สูงก็ไม่ต่ำ

หากคุณทำการวัดซ้ำด้วยเครื่องมือเดิมซ้ำแล้วซ้ำเล่า ก็ไม่ได้ช่วยให้คุณตรวจจับข้อผิดพลาดที่เป็นระบบได้แต่อย่างใด

เมื่อคุณได้ทำการหาค่าเฉลี่ยของการวัดซ้ำเพื่อลดข้อผิดพลาดแบบสุ่มแล้ว แต่ค่าที่ได้ยังคงเบี่ยงเบนจากค่าจริงที่ทราบหรือค่าอ้างอิงที่ยอมรับ คุณจำเป็นต้องลดข้อผิดพลาดที่เป็นระบบลง

เพื่อลดข้อผิดพลาดที่เป็นระบบ คุณต้องระบุประเภทของข้อผิดพลาดเหล่านั้นก่อน

คุณสามารถตรวจจับข้อผิดพลาดเหล่านี้ได้โดยการวิเคราะห์สภาพแวดล้อม เครื่องมือวัด และวิธีการของผู้ทำการทดลองอย่างละเอียดถี่ถ้วน

การทดลองแต่ละครั้งอาจพบข้อผิดพลาดได้หลายประเภท โปรดปฏิบัติตามขั้นตอนการตรวจจับและลดข้อผิดพลาดที่ระบุไว้ในตำราเรียนหรือที่อาจารย์ผู้สอนกำหนดไว้สำหรับการทดลองนั้นๆ

ข้อผิดพลาดแบบสุ่มเทียบกับข้อผิดพลาดแบบเป็นระบบ

เมื่อคุณเข้าใจเกี่ยวกับข้อผิดพลาดแบบสุ่มและข้อผิดพลาดแบบเป็นระบบแล้ว การเห็นความแตกต่างระหว่างทั้งสองแบบเคียงข้างกันจะทำให้เข้าใจได้ชัดเจนยิ่งขึ้น ลองดูตารางด้านล่างนี้

ข้อผิดพลาดร้ายแรง

ข้อผิดพลาดร้ายแรง คือ ความผิดพลาดหรือความบกพร่องที่เห็นได้ชัดเจนและใหญ่หลวง ซึ่งผู้ทำการทดลองกระทำขึ้นขณะทำการวัดหรือบันทึกผล ความผิดพลาดเหล่านี้เกิดขึ้นโดยไม่ได้ตั้งใจ

ข้อผิดพลาดร้ายแรงเรียกอีกอย่างว่า ความผิดพลาดหรือความบกพร่อง

ตัวอย่างของข้อผิดพลาดร้ายแรง:

1) หากเทอร์โมมิเตอร์วัดอุณหภูมิอ่างน้ำได้ 28 องศาเซลเซียส แต่ผู้ทำการทดลองจดบันทึกผิดพลาดเป็น 82 องศาเซลเซียส นั่นถือเป็นความผิดพลาดร้ายแรง

2) การวางจุดทศนิยมผิดขณะเขียนค่าที่วัดได้ เช่น แทนที่จะเขียน 0.52 ซม. ผู้ทำการทดลองกลับเขียน 5.2 ซม.

3) ไม้บรรทัดวัดแสดงค่าเป็นเซนติเมตร แต่ผู้ทำการทดลองบันทึกค่าผิดพลาดเป็นเมตร

วิธีลดข้อผิดพลาดร้ายแรงให้น้อยที่สุด

ข้อผิดพลาดร้ายแรงมักเป็นความผิดพลาดครั้งใหญ่ที่เห็นได้ชัดเจน ซึ่งเกิดขึ้นโดยไม่ได้ตั้งใจ จึงสังเกตได้ง่าย

ด้วยการค้นหาและแก้ไขข้อผิดพลาดเหล่านี้ คุณสามารถขจัดข้อผิดพลาดเหล่านั้นออกจากการวัดของคุณได้อย่างสมบูรณ์

วิธีการคำนวณข้อผิดพลาดในการวัด?

เราคำนวณความคลาดเคลื่อนในการวัดได้สองวิธี:

1. ข้อผิดพลาดสัมบูรณ์
2. ข้อผิดพลาดเป็นเปอร์เซ็นต์ (หรือ ข้อผิดพลาดเชิงเศษส่วน หรือ ข้อผิดพลาดสัมพัทธ์)

วิธีการคำนวณค่าความคลาดเคลื่อนสัมบูรณ์?

ค่าความคลาดเคลื่อนสัมบูรณ์ คือ ผลต่างเชิงตัวเลขระหว่างค่าที่บันทึกไว้กับค่าที่แท้จริง

มันจะบอกคุณว่าค่าที่วัดได้นั้นห่างจากค่าที่ถูกต้องมากแค่ไหน

ในทางคณิตศาสตร์

ค่าความคลาดเคลื่อนสัมบูรณ์ = ค่าที่วัดได้ − ค่าที่แท้จริง

ในความเป็นจริง เป็นไปไม่ได้ที่จะวัดค่าที่แท้จริงได้ เนื่องจากเราไม่มีเครื่องมือ สภาพแวดล้อม ผู้สังเกตการณ์ หรือผู้ทำการทดลองที่สมบูรณ์แบบ

แทนที่จะใช้วิธีนั้น เราใช้วิธีการหาค่าเฉลี่ยทางสถิติเพื่อประมาณค่าที่ใกล้เคียงกับค่าที่แท้จริงมากที่สุด โดยเราจะวัดปริมาณเดียวหลายๆ ครั้ง แล้วหาค่าเฉลี่ยของค่าเหล่านั้น

จากนั้นเราจะนำค่าเฉลี่ยนี้ไปเปรียบเทียบกับค่าที่วัดได้แต่ละค่า เพื่อประมาณค่าความคลาดเคลื่อนสัมบูรณ์ ดังนั้น เราจึงเขียนค่าความคลาดเคลื่อนสัมบูรณ์ได้ดังนี้

ค่าความคลาดเคลื่อนสัมบูรณ์ = ค่าที่วัดได้ − ค่าเฉลี่ย

วิธีคำนวณเปอร์เซ็นต์ความคลาดเคลื่อน

ในการคำนวณเปอร์เซ็นต์ความคลาดเคลื่อนของการวัด ให้หารค่าความคลาดเคลื่อนสัมบูรณ์ด้วยค่าจริง แล้วคูณผลลัพธ์สุดท้ายด้วยร้อย ในทางคณิตศาสตร์

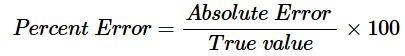
หรือ

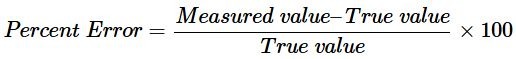
ดังที่กล่าวไว้ก่อนหน้านี้ เราไม่สามารถวัดค่าที่แท้จริงได้ในความเป็นจริง ดังนั้นแทนที่จะใช้ค่าที่แท้จริง เราจึงใช้ค่าเฉลี่ยในการคำนวณเปอร์เซ็นต์ความคลาดเคลื่อน ดังนั้นสูตรเปอร์เซ็นต์ความคลาดเคลื่อนจึงเป็นดังนี้

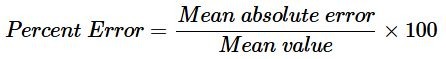
โดยที่ค่าความคลาดเคลื่อนสัมบูรณ์เฉลี่ยคำนวณได้ดังนี้

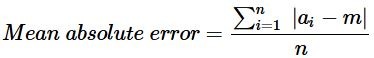
โดยที่ “ai” คือค่าที่วัดได้ และ “m” คือค่าเฉลี่ย เครื่องหมาย ∑ แทนผลรวมของค่าความคลาดเคลื่อนสัมบูรณ์ทั้งหมด และ “n” แทนจำนวนค่าที่สังเกตได้ หรือจำนวนค่าความคลาดเคลื่อนสัมบูรณ์

หากเราตัดส่วนที่เป็นเปอร์เซ็นต์ออกไป ข้อผิดพลาดนั้นจะเรียกว่าข้อผิดพลาดเชิงเศษส่วนหรือข้อผิดพลาดเชิงสัมพัทธ์

สูตรคำนวณความคลาดเคลื่อนแบบเศษส่วน:

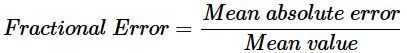
เปอร์เซ็นต์ความคลาดเคลื่อนที่ยอมรับได้ในวิชาฟิสิกส์คือเท่าไร?

เปอร์เซ็นต์ความคลาดเคลื่อนที่ยอมรับได้นั้นขึ้นอยู่กับความแม่นยำของเครื่องมือและบริบทของการทดลอง ดังนั้นจึงไม่มีกฎตายตัว

โดยทั่วไปแล้ว ค่าความคลาดเคลื่อนประมาณ 10% ถือว่ายอมรับได้ แต่หากค่าความคลาดเคลื่อนสูงกว่านั้น แสดงว่าการวัดของคุณไม่แม่นยำและจำเป็นต้องตรวจสอบอย่างละเอียด