พีชคณิตบูลีนเป็นวิธีทางคณิตศาสตร์แบบพิเศษสำหรับแสดงความสัมพันธ์ (เชิงตรรกะ) ระหว่างตัวแปร กรอบการทำงานแบบไบนารีของพีชคณิตบูลีนช่วยลดความซับซ้อนของการคำนวณทางคณิตศาสตร์ให้เหลือเพียงตรรกะจริง (1)/เท็จ (0) ซึ่งเป็นสิ่งจำเป็นสำหรับวิศวกรและโปรแกรมเมอร์

• พีชคณิตบูลีนใช้ตัวดำเนินการเช่น AND, OR และ NOT เพื่อสร้างแบบจำลองการตัดสินใจเชิงตรรกะซึ่งเป็นพื้นฐานของระบบตัวเลขทุกระบบ
• มีความจำเป็นสำหรับการสร้างเกตตรรกะที่มีประสิทธิภาพ วงจรเชิงผสม และหน่วยความจำในฮาร์ดแวร์
• เทคนิคต่างๆ เช่น แผนที่ Karnaugh และกฎบูลีนช่วยลดความซับซ้อนของวงจร ประหยัดต้นทุนและพลังงาน
• มีตรรกะแบบมีเงื่อนไข อัลกอริทึมการค้นหา และแบบสอบถามฐานข้อมูลในการพัฒนาซอฟต์แวร์

ตัวดำเนินการบูลีนพื้นฐานและเกตตรรกะ

ตัวดำเนินการบูลีนใช้สำหรับการดำเนินการทางตรรกะกับค่าบูลีน เกตตรรกะเป็นอุปกรณ์หรือวงจรทางกายภาพที่ใช้สำหรับการดำเนินการบูลีนขั้นพื้นฐาน แต่ละเกตตรรกะจะดำเนินการเฉพาะตามตรรกะบูลีน

1. ตัวดำเนินการบูลีน

• AND ( ∧ ): ตัวดำเนินการ AND จะคืนค่า True (1) เฉพาะในกรณีที่ตัวดำเนินการทั้งสองเป็น True (1) เท่านั้น
• OR (∨): ตัวดำเนินการ OR จะส่งคืนค่า True (1) หากตัวดำเนินการอย่างน้อยหนึ่งตัวเป็น True (1)
• NOT (¬): ตัวดำเนินการ NOT จะกลับค่าของตัวถูกดำเนินการ โดยจะคืนค่า True (1) หากตัวถูกดำเนินการเป็น False (0) และคืนค่า False (0) หากตัวถูกดำเนินการเป็น True (1)
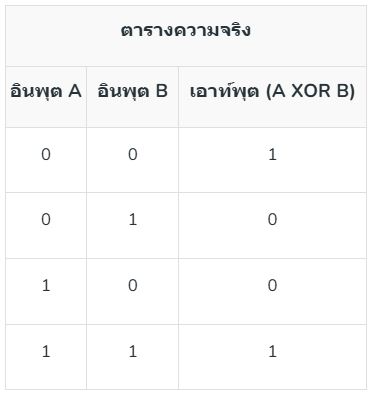
• XOR (OR แบบพิเศษ) (⊕): ตัวดำเนินการ XOR จะส่งคืนค่า True (1) หากตัวดำเนินการต่างกัน และคืนค่า False (0) หากตัวดำเนินการเหมือนกัน

2. เกตตรรกะ

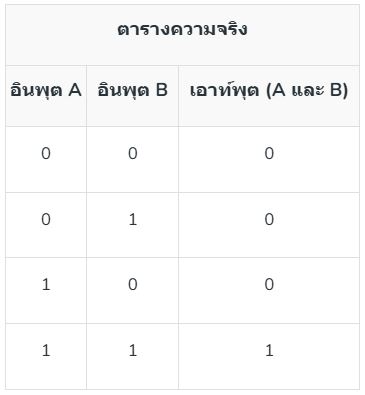
1. AND Gate:  AND gate ทำหน้าที่ดำเนินการ AND โดยจะแสดงผล 1 เฉพาะเมื่ออินพุตทั้งสองตรงกัน

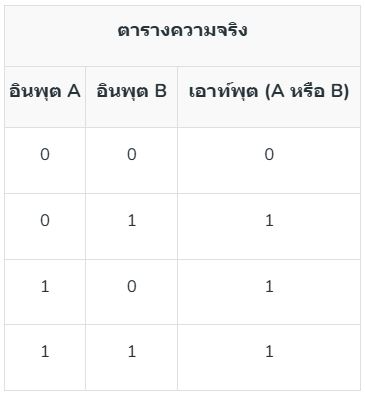
2. OR Gate:  OR gate ทำหน้าที่ OR โดยจะแสดงผล 1 หากมีอินพุตอย่างน้อยหนึ่งตัว

3. NOT Gate:  NOT gate ทำหน้าที่แทน NOT โดยจะกลับค่าอินพุต โดยเอาต์พุตจะเป็น 1 ถ้าอินพุตเป็น 0 และเอาต์พุตจะเป็น 0 ถ้าอินพุตเป็น 1

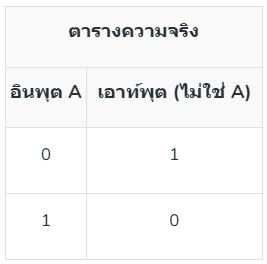
4. เกต NAND:  เกต NAND เป็นอินเวอร์สของเกต AND โดยจะส่งออกค่า 0 เฉพาะเมื่ออินพุตทั้งสองเป็น 1 มิฉะนั้นจะส่งออกค่า 1

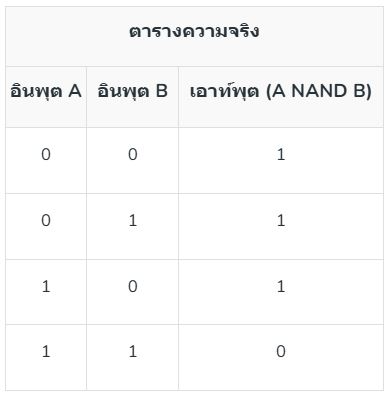
5. เกต NOR:  เกต NOR เป็นอินเวอร์สของเกต OR โดยจะส่งออกค่าเป็น 0 หากมีอินพุตอย่างน้อยหนึ่งตัวเป็น 1 หากเป็นอย่างอื่นจะส่งออกค่าเป็น 1

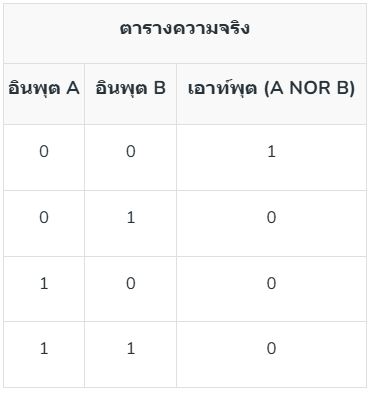
6. เกต XOR: เกต XOR ทำหน้าที่ประมวลผล XOR โดยจะแสดงผลเป็น 1 หากอินพุตต่างกัน และแสดงผลเป็น 0 หากอินพุตเหมือนกัน

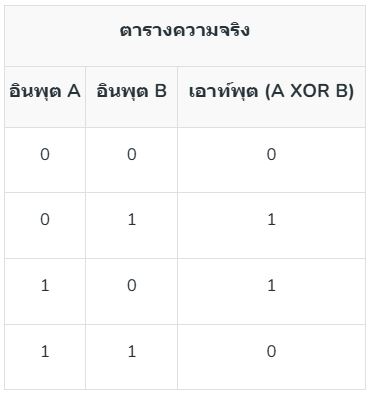
7. เกต XNOR:  เกต XNOR เป็นฟังก์ชันผกผันของการดำเนินการ XOR โดยจะบอกว่าอินพุต 1 ตัวเป็น 0 หรือต่างกัน

กฎพื้นฐานและทฤษฎีบทของพีชคณิตบูลีน

กฎและทฤษฎีบทพื้นฐานของพีชคณิตบูลีนช่วยลดความซับซ้อนของนิพจน์ตรรกะและช่วยในการออกแบบวงจรดิจิทัล กฎและทฤษฎีบทหลักของพีชคณิตบูลีนมีดังนี้:

1. กฎการสับเปลี่ยน

กฎการสับเปลี่ยนระบุว่าลำดับการรวมตัวแปรสองตัวโดยใช้ตัวดำเนินการ AND หรือ OR จะไม่ส่งผลต่อผลลัพธ์ กฎนี้ช่วยให้เราสามารถจัดเรียงพจน์ใหม่ได้โดยไม่เปลี่ยนแปลงผลลัพธ์

• กฎการสับเปลี่ยนสำหรับ AND:

A⋅B = B⋅A

ตัวอย่างเช่น:

1⋅0 = 0⋅1 = 0

• กฎการสับเปลี่ยนสำหรับ OR:

A + B = B + A

ตัวอย่างเช่น:

1 + 0 = 0 + 1 = 1

2. กฎหมายว่าด้วยการรวมกลุ่ม

กฎความสัมพันธ์ระบุว่าเมื่อรวมตัวแปรตั้งแต่สามตัวขึ้นไปโดยใช้ตัวดำเนินการ AND หรือ OR การจัดกลุ่มตัวแปรจะไม่ส่งผลต่อผลลัพธ์ กฎนี้ช่วยให้เราจัดกลุ่มพจน์ใหม่ได้โดยไม่เปลี่ยนแปลงผลลัพธ์

• กฎการเชื่อมโยงสำหรับ AND :

A⋅(B⋅C) = (A⋅B)⋅C

ตัวอย่างเช่น:

1⋅(0⋅1) = (1⋅0)⋅1 = 0

• กฎการเชื่อมโยงสำหรับ OR:

A + (B + C) = (A + B) + C

ตัวอย่างเช่น:

1 + (0 + 1) = (1 + 0) + 1 = 1

3. กฎการกระจายตัว

กฎการแจกแจงอธิบายถึงการกระจายตัวของการดำเนินการ AND และ OR ระหว่างกัน คล้ายกับการกระจายตัวของการคูณระหว่างการบวกในเลขคณิต กฎนี้ช่วยให้สามารถแยกตัวประกอบนิพจน์บูลีนได้ คล้ายกับการแยกตัวประกอบนิพจน์พีชคณิต

• กฎการแจกแจงสำหรับ AND มากกว่า OR :

A⋅(B + C) = (A⋅B) + (A⋅C)

ตัวอย่างเช่น:

1⋅(0 + 1) = (1⋅0) + (1⋅1) = 0 + 1 = 1

• กฎการแจกแจงสำหรับ OR มากกว่า AND :

A + (B⋅C) = (A + B)⋅(A + C)

ตัวอย่างเช่น:

1 + (0⋅1) = (1 + 0)⋅(1 + 1) = 1⋅1 = 1

4. กฎแห่งการระบุตัวตน

กฎเอกลักษณ์ระบุว่าตัวแปรใดๆ ที่ทำการ AND ด้วยค่า 1 หรือ OR ด้วยค่า 0 จะได้ผลลัพธ์เป็นตัวแปรเดียวกัน กฎนี้แสดงให้เห็นว่าองค์ประกอบเอกลักษณ์สำหรับการดำเนินการ AND และ OR คือ 1 และ 0 ตามลำดับ

• กฎแห่งอัตลักษณ์สำหรับ AND:

A⋅1 = A

ตัวอย่างเช่น:

1⋅1 = 1

• กฎหมายการระบุตัวตนสำหรับ OR :

A + 0 = A

ตัวอย่างเช่น:

1 + 0 = 1

5. กฎหมายเพิ่มเติม

กฎส่วนเติมเต็มเกี่ยวข้องกับการปฏิเสธตัวแปร และเกิดขึ้นเมื่อตัวแปรถูกรวมเข้ากับส่วนเติมเต็มของตัวแปรนั้น (ตรงข้าม) กฎนี้ระบุว่าตัวแปรที่ทำการ AND กับส่วนเติมเต็มของตัวแปรนั้นจะมีค่าเท่ากับ 0 เสมอ และตัวแปรที่ทำการ OR กับส่วนเติมเต็มของตัวแปรนั้นจะมีค่าเท่ากับ 1 เสมอ

• และกฎการเสริม:

A⋅A' = 0

ตัวอย่างเช่น:

1⋅1' = 1⋅0 = 0

• กฎเพิ่มเติมสำหรับ OR:

เอ+เอ' = 1

ตัวอย่างเช่น:

1 + 1' = 1 + 0 = 1

6. กฎแห่งการกลับทิศทาง

กฎของอินเวอร์สเป็นหลักการเฉพาะในพีชคณิตบูลีน ซึ่งระบุว่าส่วนเติมเต็มของส่วนเติมเต็มของตัวแปรใดๆ จะเท่ากับตัวแปรนั้นเอง

(A') = A

ตัวอย่างเช่น:

(1')' = (0)' = 1

7. ทฤษฎีบทของเดอมอร์แกน

ทฤษฎีบทของเดอมอร์แกนนำเสนอแนวทางในการลดความซับซ้อนของนิพจน์ด้วยการปฏิเสธ และมีประโยชน์มากในการออกแบบวงจรดิจิทัล

ทฤษฎีบทแรกของเดอ มอร์แกน: การปฏิเสธการดำเนินการ AND จะเท่ากับการดำเนินการ OR ของการปฏิเสธตัวดำเนินการ

(A⋅B)' = A' + B'

ตัวอย่างเช่น:

การแสดงออก: (1⋅0)'

ลดรูป: 1' + 0' = 0 + 1 = 1

ทฤษฎีบทที่สองของเดอ มอร์แกน: การปฏิเสธการดำเนินการ OR จะเท่ากับการดำเนินการ AND ของการปฏิเสธตัวดำเนินการ

(A+B)' = A'⋅B'

ตัวอย่างเช่น:

นิพจน์: (1 + 0)'

ลดรูป: 1'⋅0' = 0⋅1 = 0

ตัวอย่างพีชคณิตบูลีน

มาแก้สมการบูลีนกัน:

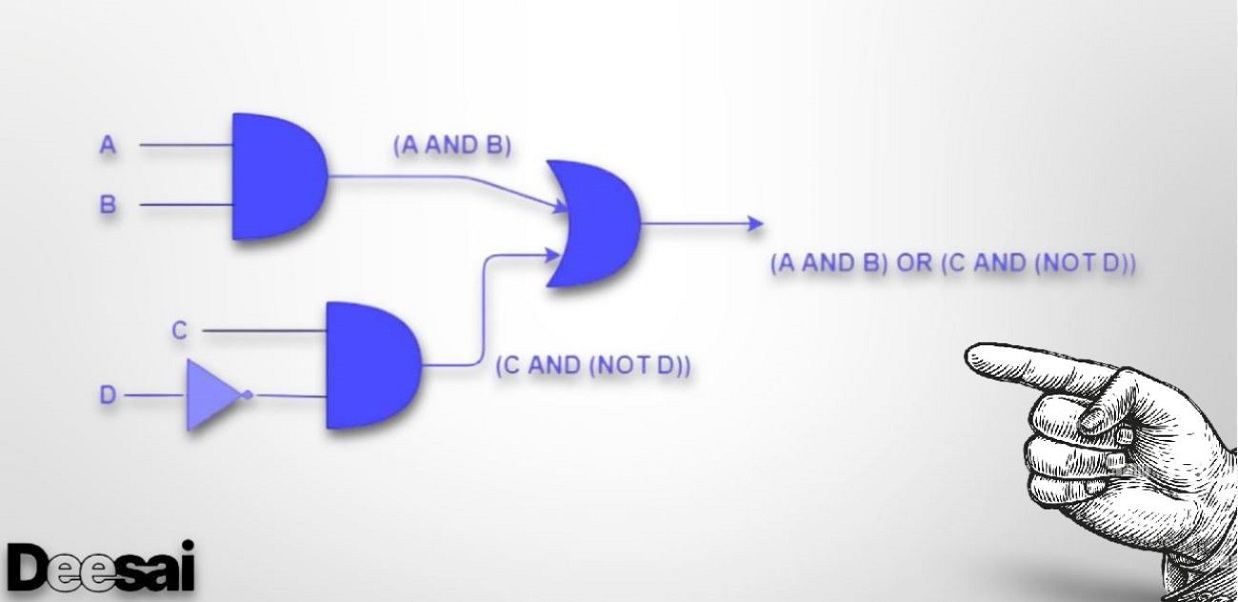
(A ∧ B) ∨ (C ∧ (¬D)) 

ให้ A = B = 1, C = 0, D = 0

วิธีแก้: แทนที่นิพจน์ด้วยค่าที่กำหนดทีละส่วน

• (A ∧ B) = (1 ∧ 1) = 1
• (C ∧ (¬D)) = (0 ∧ (¬0)) = (0 ∧ 1) = 0
• (A ∧ B) ∨ (C ∧ (¬D)) = (1 ∨ 0) = 1

ดังนั้นคำตอบสุดท้ายสำหรับนิพจน์บูลีนที่กำหนดคือ 1

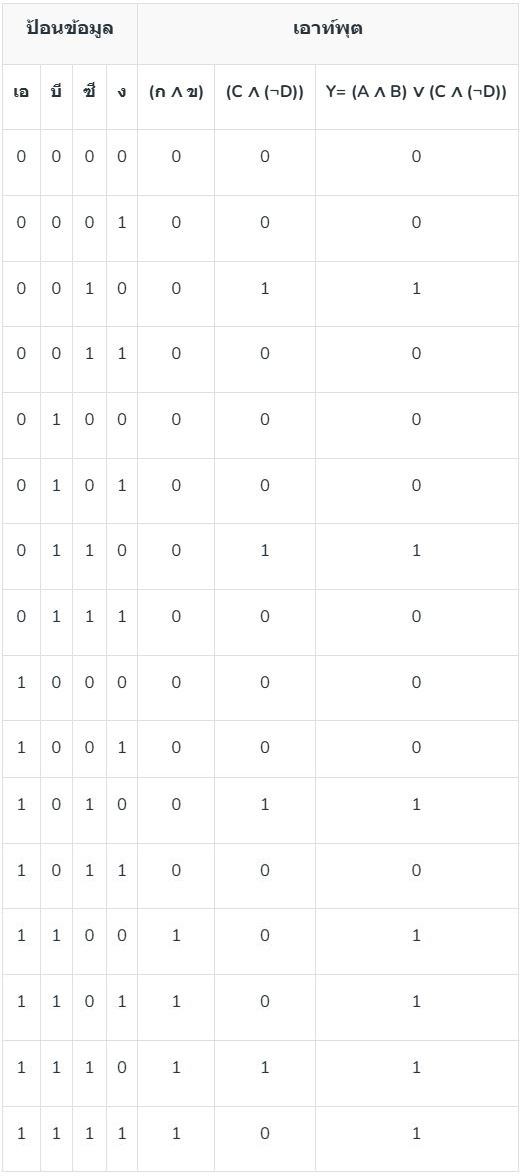
มาทำความเข้าใจกันโดยใช้ตารางความจริง สมมติว่า:

Y= (A ∧ B) ∨ (C ∧ (¬D)) 

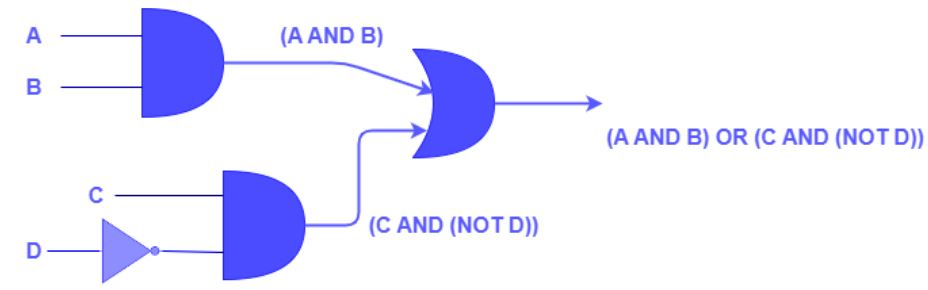
แผนภาพวงจรตรรกะของตัวอย่างข้างต้น:

การประยุกต์ใช้พีชคณิตบูลีน

1. การออกแบบวงจรดิจิทัล: พีชคณิตบูลีนช่วยลดความซับซ้อนในการออกแบบวงจรเชิงผสมและเชิงลำดับ เช่น วงจรบวก วงจรมัลติเพล็กเซอร์ วงจรฟลิปฟล็อป และวงจรรีจิสเตอร์ ช่วยเพิ่มประสิทธิภาพการทำงานและการใช้งานเกต
2. การลดความซับซ้อนของนิพจน์ตรรกะ: พีชคณิตบูลีนช่วยลดความซับซ้อนของนิพจน์ตรรกะ ลดจำนวนเกตที่จำเป็น และปรับปรุงประสิทธิภาพของวงจรและการใช้พลังงาน
3. การออกแบบวงจรเลขคณิต: ใช้สำหรับออกแบบตัวบวก ตัวลบ ตัวคูณ และตัวหารแบบไบนารี ซึ่งจำเป็นสำหรับการดำเนินการเลขคณิตแบบไบนารีในระบบตัวเลข
4. การออกแบบส่วนประกอบหน่วยความจำ: พีชคณิตบูลีนช่วยในการออกแบบหน่วยความจำ เช่น ฟลิปฟล็อป แลตช์ และรีจิสเตอร์ ซึ่งช่วยในการจัดเก็บข้อมูลและจัดการการเปลี่ยนสถานะในวงจรแบบต่อเนื่อง
5. การตรวจจับและแก้ไขข้อผิดพลาด: ใช้ในเทคนิคการตรวจจับข้อผิดพลาด (เช่น การตรวจสอบพาริตี้) และการแก้ไขข้อผิดพลาด (เช่น รหัสแฮมมิง) เพื่อให้แน่ใจว่าข้อมูลมีความสมบูรณ์ในระบบการสื่อสาร
6. ระบบควบคุมและตัวควบคุมลอจิก: พีชคณิตบูลีนมีบทบาทสำคัญในการออกแบบลอจิกควบคุมสำหรับระบบต่างๆ เช่น เครื่องจักรสถานะจำกัด (FSM) และตัวควบคุมลอจิกที่ตั้งโปรแกรมได้ (PLC) ซึ่งช่วยจัดการกระบวนการอัตโนมัติ
7. การเพิ่มประสิทธิภาพการออกแบบวงจร: ช่วยลดความซับซ้อนของวงจรดิจิทัล ลดจำนวนเกต ลดพื้นที่ และปรับปรุงประสิทธิภาพการใช้พลังงานใน IC, FPGA และ ASIC
8. ระบบการเข้ารหัสและความปลอดภัย: พีชคณิตบูลีนถูกนำมาใช้ในการออกแบบวงจรการเข้ารหัสและถอดรหัส รองรับการส่งข้อมูลที่ปลอดภัยและการตรวจสอบสิทธิ์ในระบบความปลอดภัยดิจิทัล
9. การประมวลผลสัญญาณดิจิทัล (DSP): ใช้ในการประมวลผลสัญญาณดิจิทัลสำหรับงานต่างๆ เช่น การกรอง การเข้ารหัส และการแปลงเสียง วิดีโอ และสัญญาณอื่นๆ เป็นรูปแบบดิจิทัล