การแนะนำ 

วิธีหนึ่งที่มีประสิทธิภาพในการกรองสัญญาณรบกวนจากแหล่งจ่ายไฟความถี่สูง และแบ่งปันรางจ่ายแรงดันไฟฟ้าที่คล้ายคลึงกัน (เช่น รางอนาล็อกและดิจิทัลสำหรับไอซีสัญญาณผสม) ได้อย่างหมดจด ขณะเดียวกันก็รักษาการแยกความถี่สูงระหว่างรางที่ใช้ร่วมกัน คือการใช้ลูกปัดเฟอร์ไรต์ ลูกปัดเฟอร์ไรต์เป็นอุปกรณ์แบบพาสซีฟที่กรองพลังงานสัญญาณรบกวนความถี่สูงในช่วงความถี่กว้าง ลูกปัดเฟอร์ไรต์จะต้านทานในช่วงความถี่ที่ต้องการ และกระจายพลังงานสัญญาณรบกวนในรูปของความร้อน ลูกปัดเฟอร์ไรต์จะเชื่อมต่อแบบอนุกรมกับรางจ่ายไฟ และมักจะเชื่อมต่อกับตัวเก็บประจุเพื่อต่อลงกราวด์ที่ด้านใดด้านหนึ่งของลูกปัด วิธีนี้จะสร้างเครือข่ายตัวกรองความถี่ต่ำ ซึ่งจะช่วยลดสัญญาณรบกวนจากแหล่งจ่ายไฟความถี่สูงลงไปอีก

อย่างไรก็ตาม การใช้ลูกปัดเฟอร์ไรต์อย่างไม่เหมาะสมในการออกแบบระบบอาจนำไปสู่ปัญหาที่เป็นอันตรายได้ ตัวอย่างเช่น การสั่นพ้องที่ไม่พึงประสงค์อันเนื่องมาจากการรวมลูกปัดเข้ากับตัวเก็บประจุแยกสัญญาณสำหรับการกรองความถี่ต่ำ และผลกระทบของกระแสไบอัสกระแสตรงที่ส่งผลต่อความสามารถในการป้องกันคลื่นแม่เหล็กไฟฟ้าของลูกปัด หากเข้าใจและพิจารณาพฤติกรรมของลูกปัดเฟอร์ไรต์อย่างถูกต้อง ปัญหาเหล่านี้ก็สามารถหลีกเลี่ยงได้

บทความนี้จะกล่าวถึงข้อควรพิจารณาสำคัญที่ผู้ออกแบบระบบจำเป็นต้องตระหนักเมื่อใช้เม็ดเฟอร์ไรต์ในระบบจ่ายไฟ เช่น อิมพีแดนซ์เทียบกับลักษณะความถี่ที่กระแสไบอัส DC เปลี่ยนแปลง และผลกระทบจากเรโซแนนซ์ LC ที่ไม่พึงประสงค์ เพื่อแก้ไขปัญหาเรโซแนนซ์ที่ไม่พึงประสงค์ จะมีการอธิบายเทคนิคการหน่วงสัญญาณ และการเปรียบเทียบประสิทธิภาพของวิธีการหน่วงสัญญาณแต่ละวิธี

อุปกรณ์ที่ใช้สาธิตผลกระทบของลูกปัดเฟอร์ไรต์ในฐานะตัวกรองเอาต์พุตคือตัวควบคุมการสลับกระแสตรงเป็นกระแสตรงขนาด 2 แอมป์/1.2 แอมป์ ที่มีเอาต์พุตบวกและลบแยกกัน ( ADP5071 ) ลูกปัดเฟอร์ไรต์ที่ใช้ในบทความนี้ส่วนใหญ่เป็นแบบติดตั้งบนพื้นผิวชนิดชิป

แบบจำลองและการจำลองแบบง่ายของลูกปัดเฟอร์ไรต์ 

เฟอร์ไรต์บีดสามารถจำลองเป็นวงจรแบบง่ายที่ประกอบด้วยตัวต้านทาน ตัวเหนี่ยวนำ และตัวเก็บประจุ ดังแสดงในรูปที่ 1a โดย RDC สอดคล้องกับความต้านทานกระแสตรงของบีด CPAR, LBEAD และ RAC (ตามลำดับ) คือความจุปรสิต เหนี่ยวนำบีด และความต้านทานกระแสสลับ (การสูญเสียแกนกระแสสลับ) ที่เกี่ยวข้องกับบีด

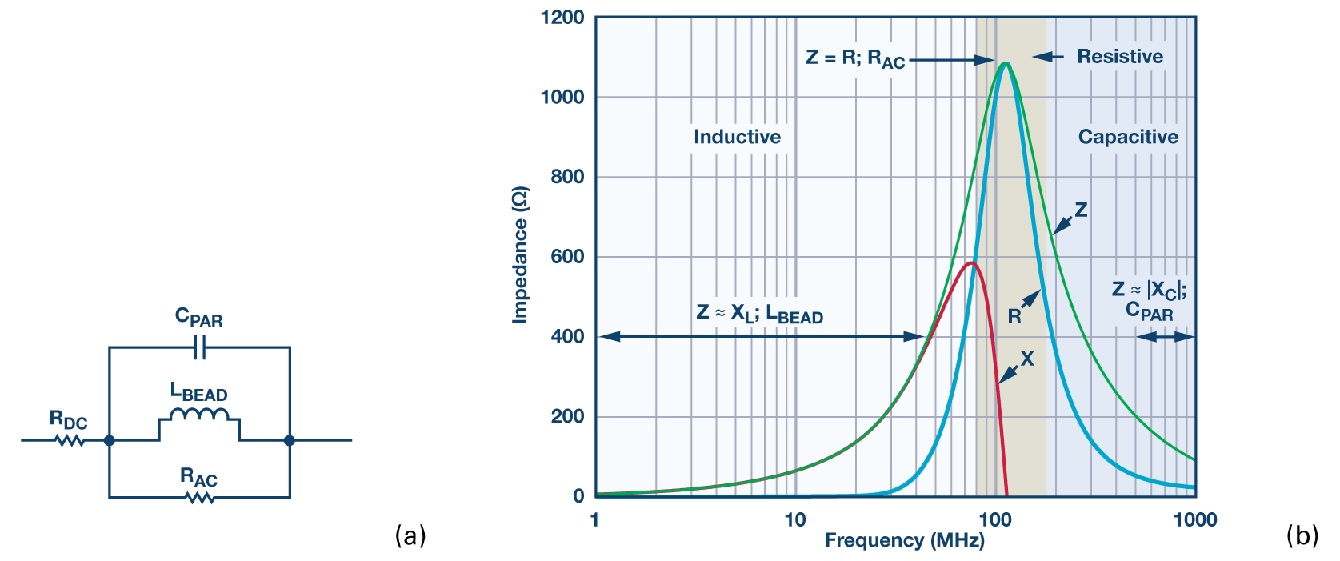
ลูกปัดเฟอร์ไรต์แบ่งตามบริเวณการตอบสนองสามส่วน ได้แก่ เหนี่ยวนำ ต้านทาน และเก็บประจุ บริเวณเหล่านี้สามารถกำหนดได้โดยดูจากกราฟ ZRX (แสดงในรูปที่ 1b) โดยที่ Z คืออิมพีแดนซ์ R คือความต้านทาน และ X คือรีแอกแตนซ์ของลูกปัด เพื่อลดสัญญาณรบกวนความถี่สูง ลูกปัดจะต้องอยู่ในบริเวณรีแอกแตนซ์ ซึ่งเหมาะอย่างยิ่งสำหรับการใช้งานในการกรองสัญญาณรบกวนแม่เหล็กไฟฟ้า (EMI) ส่วนประกอบนี้ทำหน้าที่เหมือนตัวต้านทาน ซึ่งทำหน้าที่ขัดขวางสัญญาณรบกวนความถี่สูงและกระจายออกไปในรูปของความร้อน บริเวณรีแอกแตนซ์จะเกิดขึ้นหลังจากความถี่ครอสโอเวอร์ของลูกปัด (X = R) จนถึงจุดที่ลูกปัดกลายเป็นแบบเก็บประจุ จุดเก็บประจุนี้เกิดขึ้นที่ความถี่ซึ่งค่าสัมบูรณ์ของรีแอกแตนซ์แบบเก็บประจุ (–X) เทียบเท่ากับ R

ในบางกรณี สามารถใช้แบบจำลองวงจรที่เรียบง่ายเพื่อประมาณค่าลักษณะเฉพาะของอิมพีแดนซ์ของเม็ดเฟอร์ไรต์ได้สูงสุดถึงช่วงต่ำกว่า GHz

ตัวอย่างใช้บีดเฟอร์ไรต์หลายชั้น BMB2A1000LN2 ของ Tyco Electronics รูปที่ 1b แสดงค่าการตอบสนอง ZRX ที่วัดได้ของ BMB2A1000LN2 สำหรับกระแสไบอัสศูนย์ DC โดยใช้เครื่องวิเคราะห์อิมพีแดนซ์

สำหรับภูมิภาคบนพล็อต ZRX ที่วัดได้ ซึ่งลูกปัดปรากฏว่าเหนี่ยวนำมากที่สุด (Z ≈ XL; LBEAD) เหนี่ยวนำลูกปัดจะคำนวณได้จากสมการต่อไปนี้:

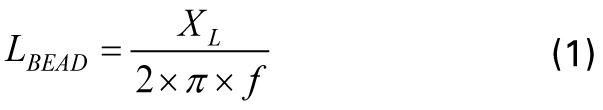
ที่ไหน:

f คือจุดความถี่ ณ ตำแหน่งใดก็ได้ในบริเวณที่ลูกปัดปรากฏเป็นแบบเหนี่ยวนำ ในตัวอย่างนี้ f = 30.7 MHz XL คือค่ารีแอกแตนซ์ที่ 30.7 MHz ซึ่งมีค่าเท่ากับ 233 Ω

สมการที่ 1 ให้ค่าเหนี่ยวนำ (LBEAD) ที่ 1.208 µH

สำหรับภูมิภาคที่ลูกปัดปรากฏว่ามีความจุมากที่สุด (Z ≈ |XC|; CPAR) ความจุปรสิตจะคำนวณได้จากสมการต่อไปนี้:

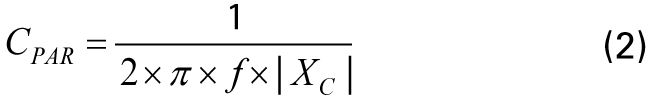
ที่ไหน:

f คือจุดความถี่ ณ ตำแหน่งใดก็ได้ในบริเวณที่บีดปรากฏเป็นตัวเก็บประจุ ในตัวอย่างนี้ f  = 803 MHz | XC | คือรีแอคแตนซ์ที่ความถี่ 803 MHz ซึ่งเท่ากับ 118.1 Ω

สมการที่ 2 ให้ค่าความจุปรสิต (CPAR) ที่ 1.678 pF

ค่าความต้านทานกระแสตรง (RDC) ซึ่งเท่ากับ 300 mΩ ได้มาจากเอกสารข้อมูลของผู้ผลิต ค่าความต้านทานกระแสสลับ (RAC) คือค่าอิมพีแดนซ์สูงสุดที่บีดดูเหมือนจะเป็นค่าความต้านทานเพียงอย่างเดียว คำนวณ RAC โดยการลบ RDC ออกจาก Z เนื่องจาก RDC มีค่าน้อยมากเมื่อเทียบกับค่าอิมพีแดนซ์สูงสุด จึงสามารถละเลยค่านี้ได้ ดังนั้น ในกรณีนี้ RAC จึงมีค่าเท่ากับ 1.082 kΩ เครื่องมือจำลองวงจร ADIsimPE ที่ขับเคลื่อนโดย SIMetrix/SIMPLIS ถูกใช้เพื่อสร้างค่าอิมพีแดนซ์เทียบกับการตอบสนองความถี่ รูปที่ 2a แสดงแบบจำลองวงจรพร้อมค่าที่คำนวณได้ และรูปที่ 2b แสดงทั้งค่าที่วัดได้จริงและค่าที่จำลอง ในตัวอย่างนี้ เส้นโค้งอิมพีแดนซ์จากแบบจำลองวงจรมีค่าใกล้เคียงกับเส้นโค้งที่วัดได้มาก

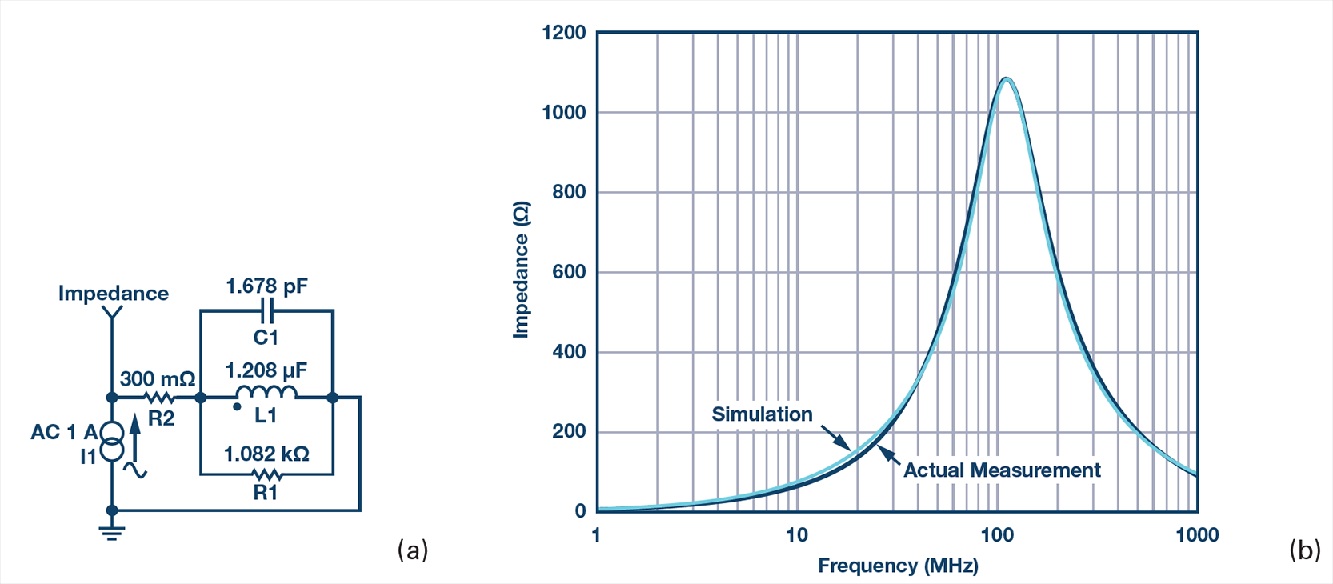
แบบจำลองเฟอร์ไรต์บีดมีประโยชน์ในการออกแบบและวิเคราะห์วงจรกรองสัญญาณรบกวน ตัวอย่างเช่น การประมาณค่าความเหนี่ยวนำของบีดอาจเป็นประโยชน์ในการกำหนดจุดตัดความถี่เรโซแนนซ์เมื่อใช้ร่วมกับตัวเก็บประจุแบบแยกตัวในเครือข่ายตัวกรองความถี่ต่ำ อย่างไรก็ตาม แบบจำลองวงจรที่ระบุในบทความนี้เป็นการประมาณค่าที่มีกระแสไบอัส DC เป็นศูนย์ แบบจำลองนี้อาจเปลี่ยนแปลงไปตามกระแสไบอัส DC และในกรณีอื่นๆ จำเป็นต้องใช้แบบจำลองที่ซับซ้อนกว่า

การพิจารณากระแสไบแอส DC 

การเลือกบีดเฟอร์ไรต์ที่เหมาะสมสำหรับการใช้งานด้านพลังงานต้องพิจารณาอย่างรอบคอบไม่เพียงแต่แบนด์วิดท์ของตัวกรองเท่านั้น แต่ยังรวมถึงลักษณะความต้านทานของบีดเมื่อเทียบกับกระแสไบอัส DC ด้วย ในกรณีส่วนใหญ่ ผู้ผลิตจะระบุค่าอิมพีแดนซ์ของบีดที่ 100 MHz และเผยแพร่เอกสารข้อมูลพร้อมกราฟตอบสนองความถี่ที่กระแสไบอัส DC เป็นศูนย์ อย่างไรก็ตาม เมื่อใช้บีดเฟอร์ไรต์สำหรับการกรองแหล่งจ่ายไฟ กระแสโหลดที่ไหลผ่านบีดเฟอร์ไรต์จะไม่เป็นศูนย์ และเมื่อกระแสไบอัส DC เพิ่มขึ้นจากศูนย์ พารามิเตอร์ทั้งหมดเหล่านี้จะเปลี่ยนแปลงอย่างมีนัยสำคัญ

เมื่อกระแสไบแอส DC เพิ่มขึ้น วัสดุแกนจะเริ่มอิ่มตัว ซึ่งส่งผลให้ความเหนี่ยวนำของเม็ดเฟอร์ไรต์ลดลงอย่างมาก ระดับความอิ่มตัวของความเหนี่ยวนำจะแตกต่างกันไปขึ้นอยู่กับวัสดุที่ใช้ทำแกนของส่วนประกอบ รูปที่ 3a แสดงความสัมพันธ์ระหว่างไบแอส DC ทั่วไปของความเหนี่ยวนำของเม็ดเฟอร์ไรต์สองเม็ด เมื่อกระแสไบแอส DC เพิ่มขึ้น 50% ความเหนี่ยวนำจะลดลงสูงสุดถึง 90%

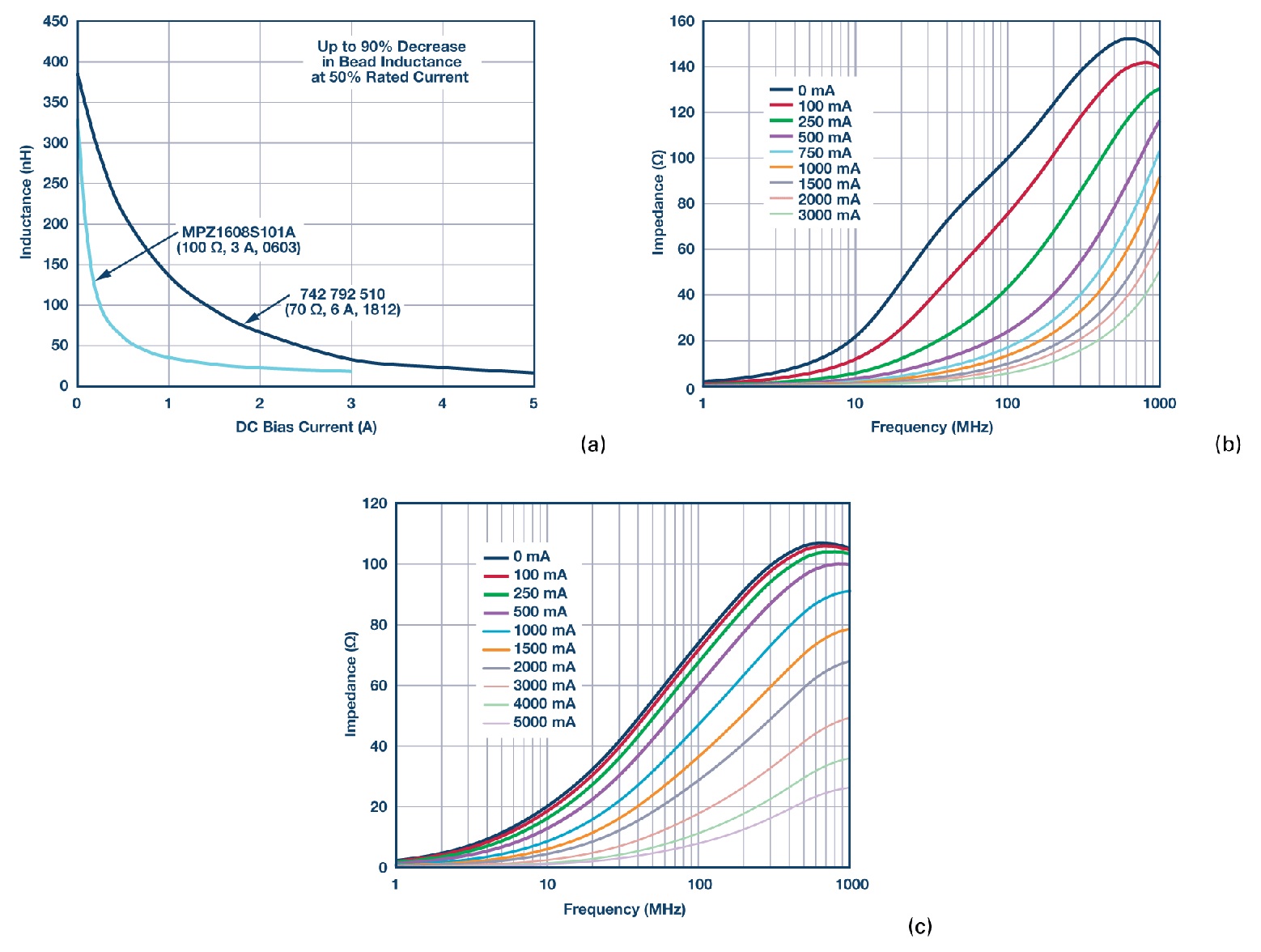
เพื่อการกรองสัญญาณรบกวนจากแหล่งจ่ายไฟอย่างมีประสิทธิภาพ แนวทางการออกแบบคือการใช้เม็ดเฟอร์ไรต์ที่ประมาณ 20% ของกระแสไฟฟ้ากระแสตรงที่กำหนด ดังที่แสดงในสองตัวอย่างนี้ ค่าเหนี่ยวนำที่ 20% ของกระแสไฟฟ้าที่กำหนดจะลดลงเหลือประมาณ 30% สำหรับเม็ด 6 A และเหลือประมาณ 15% สำหรับเม็ด 3 A พิกัดกระแสของเม็ดเฟอร์ไรต์เป็นตัวบ่งชี้กระแสไฟฟ้าสูงสุดที่อุปกรณ์สามารถรับได้เมื่ออุณหภูมิเพิ่มขึ้นตามที่กำหนด และไม่ใช่จุดทำงานจริงสำหรับการกรอง

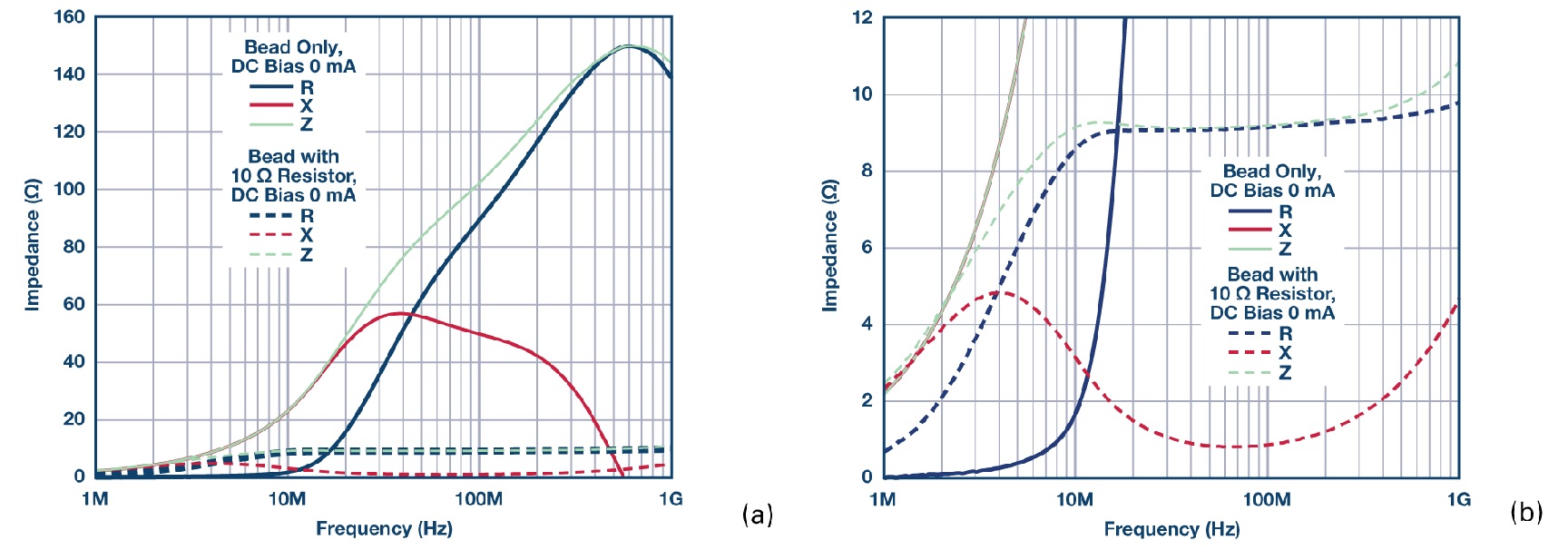
นอกจากนี้ ผลของกระแสไบอัสกระแสตรงยังสามารถสังเกตได้จากการลดค่าอิมพีแดนซ์เหนือความถี่ ซึ่งส่งผลให้ประสิทธิภาพของเม็ดเฟอร์ไรต์และความสามารถในการกำจัด EMI ลดลง รูปที่ 3b และรูปที่ 3c แสดงให้เห็นว่าอิมพีแดนซ์ของเม็ดเฟอร์ไรต์แปรผันตามกระแสไบอัสกระแสตรง การใช้กระแสไฟฟ้าเพียง 50% ของค่าที่กำหนด อิมพีแดนซ์ที่มีประสิทธิภาพที่ความถี่ 100 MHz ลดลงอย่างมากจาก 100 Ω เหลือ 10 Ω สำหรับ TDK MPZ1608S101A (100 Ω, 3 A, 0603) และจาก 70 Ω เหลือ 15 Ω สำหรับ Würth Elektronik 742 792 510 (70 Ω, 6 A, 1812)

นักออกแบบระบบต้องตระหนักถึงผลกระทบของกระแสไบอัส DC ต่อความเหนี่ยวนำของลูกปัดและอิมพีแดนซ์ที่มีประสิทธิภาพ เนื่องจากสิ่งนี้อาจมีความสำคัญในแอปพลิเคชันที่ต้องการกระแสไฟฟ้าจ่ายสูง

เอฟเฟกต์เรโซแนนซ์ LC 

จุดสูงสุดของเรโซแนนซ์สามารถทำได้เมื่อใช้ลูกปัดเฟอร์ไรต์ร่วมกับตัวเก็บประจุแบบแยกส่วน ผลกระทบที่มักถูกมองข้ามนี้อาจเป็นอันตราย เพราะอาจขยายสัญญาณริปเปิลและสัญญาณรบกวนในระบบที่กำหนดแทนที่จะลดทอนสัญญาณรบกวน ในหลายกรณี จุดสูงสุดนี้เกิดขึ้นรอบความถี่สวิตชิ่งที่นิยมใช้ในตัวแปลง DC-to-DC

จุดสูงสุดเกิดขึ้นเมื่อความถี่เรโซแนนซ์ของเครือข่ายตัวกรองความถี่ต่ำผ่าน ซึ่งเกิดจากความเหนี่ยวนำของเม็ดเฟอร์ไรต์และความจุแยกตัว Q สูง มีค่าต่ำกว่าความถี่ครอสโอเวอร์ของเม็ด ตัวกรองที่ได้จะถูกลดทอนสัญญาณลง รูปที่ 4a แสดงกราฟอิมพีแดนซ์เทียบกับความถี่ที่วัดได้ของ TDK MPZ1608S101A ส่วนประกอบตัวต้านทาน ซึ่งใช้ในการกระจายพลังงานที่ไม่ต้องการ จะไม่มีความสำคัญจนกว่าจะถึงช่วงประมาณ 20 MHz ถึง 30 MHz ที่ต่ำกว่าความถี่นี้ เม็ดเฟอร์ไรต์ยังคงมีค่า Q สูงมากและทำหน้าที่เป็นตัวเหนี่ยวนำในอุดมคติ ความถี่เรโซแนนซ์ LC สำหรับตัวกรองเม็ดทั่วไปโดยทั่วไปจะอยู่ในช่วง 0.1 MHz ถึง 10 MHz สำหรับความถี่สวิตชิ่งทั่วไปในช่วง 300 kHz ถึง 5 MHz จำเป็นต้องมีการหน่วงสัญญาณเพิ่มเติมเพื่อลดค่า Q ของตัวกรอง

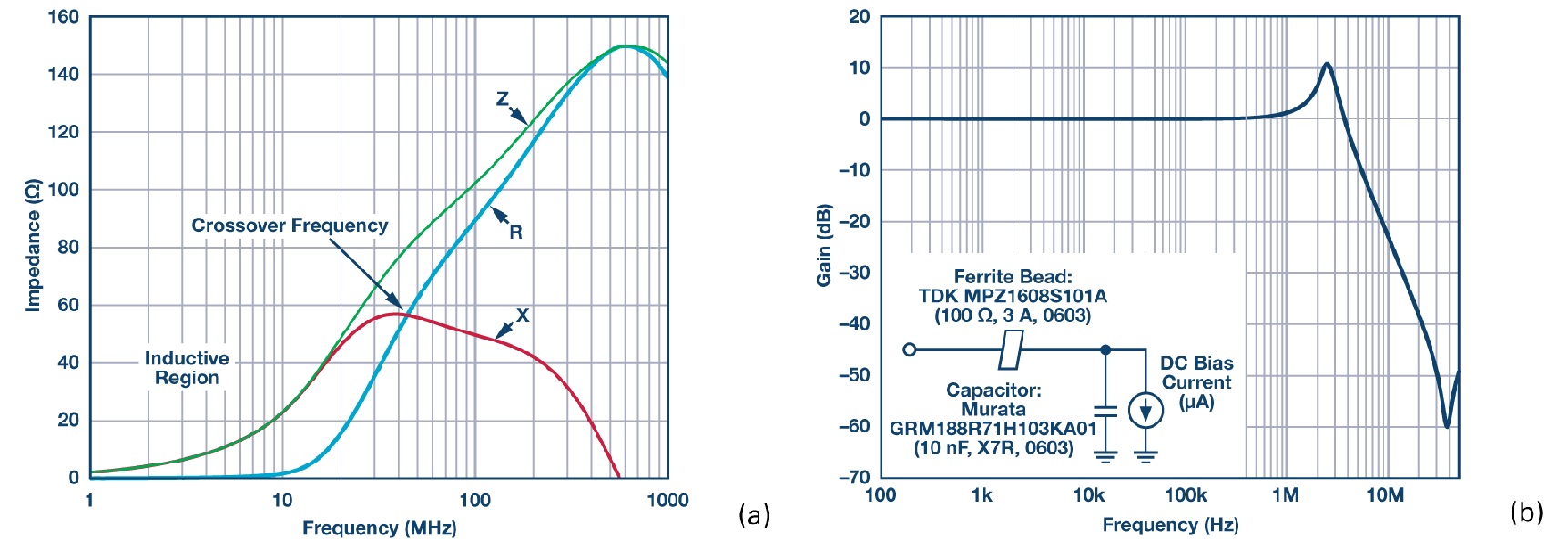
ตัวอย่างของเอฟเฟกต์นี้ รูปที่ 4b แสดงการตอบสนองความถี่ S21 ของบีดและตัวกรองความถี่ต่ำผ่านตัวเก็บประจุ ซึ่งแสดงเอฟเฟกต์พีคกิ้ง บีดเฟอร์ไรต์ที่ใช้คือ TDK MPZ1608S101A (100 Ω, 3 A, 0603) และตัวเก็บประจุแยกที่ใช้คือตัวเก็บประจุเซรามิก ESR ต่ำ Murata GRM188R71H103KA01 (10 nF, X7R, 0603) กระแสโหลดอยู่ในช่วงไมโครแอมแปร์

ฟิลเตอร์บีดเฟอร์ไรต์แบบไม่มีการหน่วงสัญญาณสามารถแสดงค่าพีคได้ตั้งแต่ประมาณ 10 เดซิเบล ถึงประมาณ 15 เดซิเบล ขึ้นอยู่กับค่า Q ของวงจรฟิลเตอร์ ในรูปที่ 4b ค่าพีคจะเกิดขึ้นที่ความถี่ประมาณ 2.5 เมกะเฮิรตซ์ โดยมีเกนมากถึง 10 เดซิเบล

นอกจากนี้ สัญญาณเกนยังสามารถเห็นได้ตั้งแต่ 1 MHz ถึง 3.5 MHz จุดสูงสุดนี้เป็นปัญหาหากเกิดขึ้นในย่านความถี่ที่ตัวควบคุมการสวิตชิ่งทำงานอยู่ จุดสูงสุดนี้จะขยายสัญญาณรบกวนจากการสวิตชิ่งที่ไม่ต้องการ ซึ่งอาจส่งผลเสียต่อประสิทธิภาพของโหลดที่มีความละเอียดอ่อน เช่น ลูปล็อกเฟส (PLL), ออสซิลเลเตอร์ควบคุมแรงดันไฟฟ้า (VCO) และตัวแปลงอนาล็อกเป็นดิจิทัลความละเอียดสูง (ADC) ผลลัพธ์ที่แสดงในรูปที่ 4b นำมาจากโหลดที่เบามาก (ในช่วงไมโครแอมแปร์) แต่สามารถนำไปประยุกต์ใช้งานได้จริงในส่วนของวงจรที่ต้องการกระแสโหลดเพียงไม่กี่ไมโครแอมแปร์ถึง 1 มิลลิแอมป์ หรือในส่วนที่ปิดเครื่องเพื่อประหยัดพลังงานในบางโหมดการทำงาน จุดสูงสุดที่อาจเกิดขึ้นนี้จะสร้างสัญญาณรบกวนเพิ่มเติมในระบบ ซึ่งอาจทำให้เกิดสัญญาณรบกวนข้ามสัญญาณที่ไม่พึงประสงค์ได้

ตัวอย่าง รูปที่ 5 แสดงวงจรประยุกต์ ADP5071 ที่มีฟิลเตอร์บีดติดตั้งใช้งาน และรูปที่ 6 แสดงกราฟสเปกตรัมที่เอาต์พุตบวก ความถี่สวิตชิ่งตั้งไว้ที่ 2.4 MHz แรงดันไฟฟ้าขาเข้า 9 V แรงดันไฟฟ้าขาออก 16 V และกระแสโหลด 5 mA

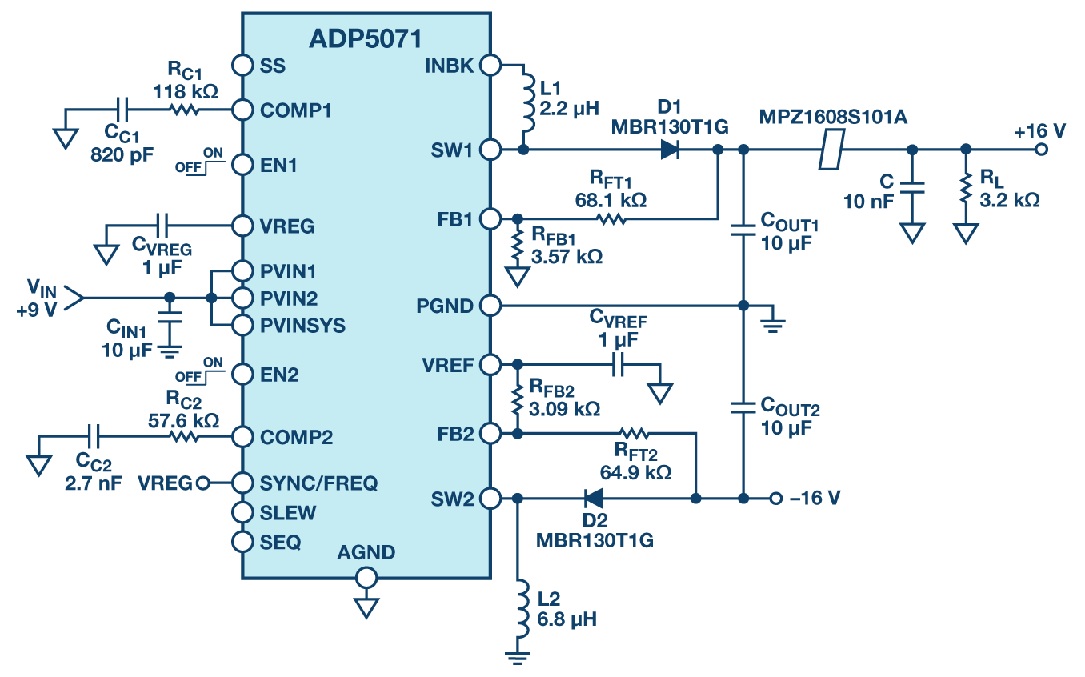
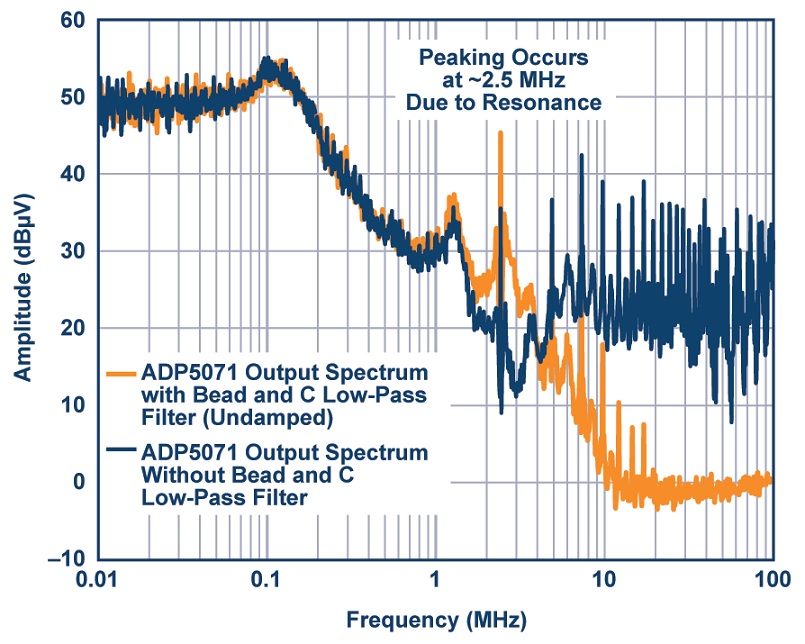
พีคเรโซแนนซ์เกิดขึ้นที่ประมาณ 2.5 MHz เนื่องจากความเหนี่ยวนำของบีดและตัวเก็บประจุเซรามิก 10 nF แทนที่จะลดทอนความถี่ริปเปิลพื้นฐานที่ 2.4 MHz กลับมีเกนเพิ่มขึ้น 10 dB

ปัจจัยอื่นๆ ที่มีผลต่อค่าพีคเรโซแนนซ์ ได้แก่ อิมพีแดนซ์อนุกรมและอิมพีแดนซ์โหลดของฟิลเตอร์เฟอร์ไรต์บีด ค่าพีคจะลดลงอย่างมากและถูกหน่วงเพื่อให้ความต้านทานของแหล่งกำเนิดสูงขึ้น อย่างไรก็ตาม การควบคุมโหลดจะด้อยลงด้วยวิธีการนี้ ทำให้ไม่สมจริงในทางปฏิบัติ แรงดันเอาต์พุตจะลดลงเมื่อกระแสโหลดลดลงเนื่องจากความต้านทานอนุกรมลดลง อิมพีแดนซ์โหลดยังส่งผลต่อการตอบสนองของพีคอีกด้วย ค่าพีคจะแย่ลงในสภาวะโหลดเบา

วิธีการลดแรงสั่นสะเทือน 

หัวข้อนี้จะอธิบายวิธีการลดทอนสามวิธีที่วิศวกรระบบสามารถใช้เพื่อลดระดับพีคเรโซแนนซ์ได้อย่างมีนัยสำคัญ (ดูรูปที่ 7)

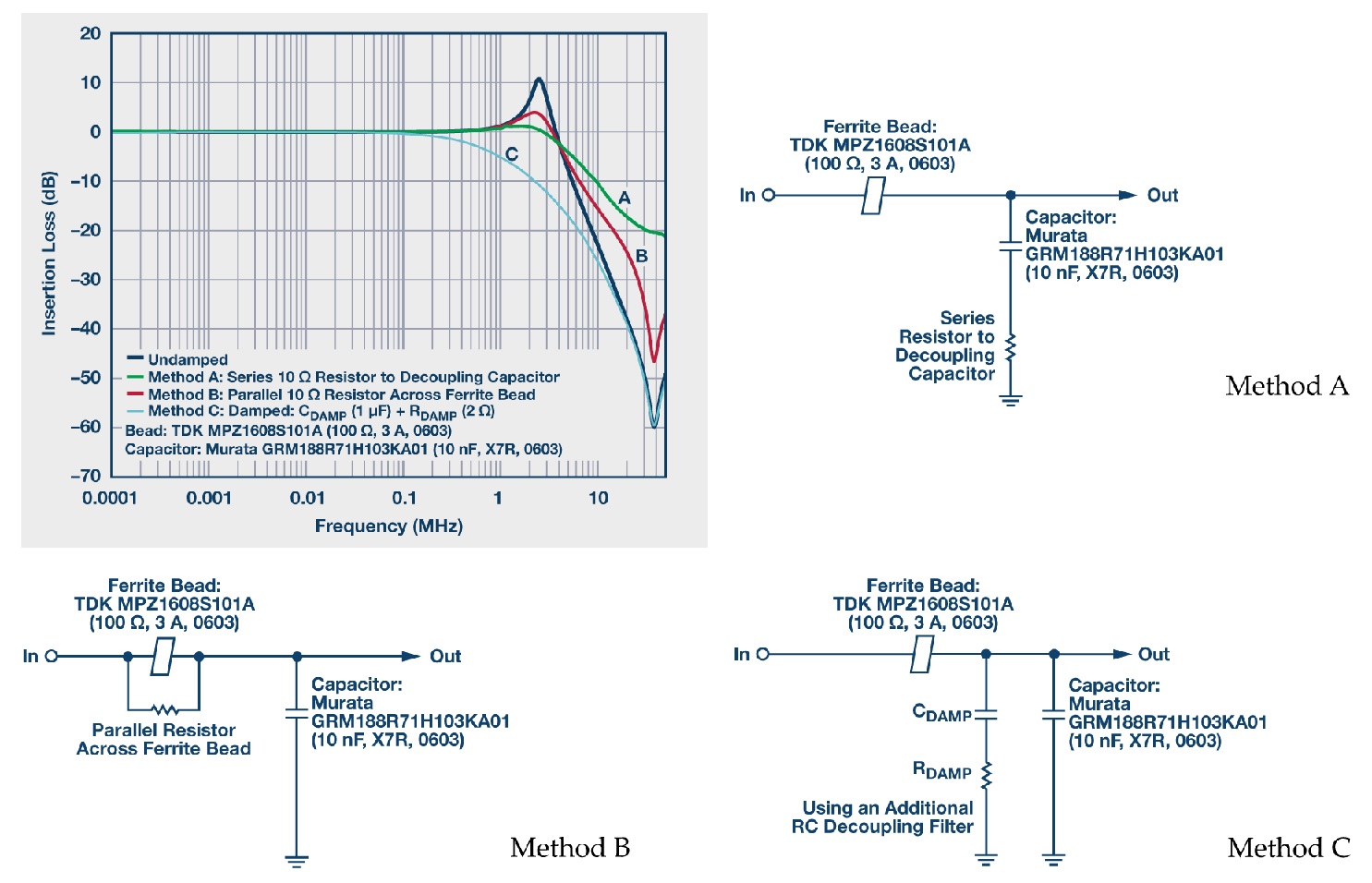
วิธี A ประกอบด้วยการเพิ่มตัวต้านทานแบบอนุกรมลงในเส้นทางของตัวเก็บประจุแบบแยกตัว ซึ่งจะช่วยลดการสั่นพ้องของระบบ แต่จะทำให้ประสิทธิภาพของบายพาสลดลงที่ความถี่สูง วิธี B ประกอบด้วยการเพิ่มตัวต้านทานแบบขนานขนาดเล็กข้ามบีดเฟอร์ไรต์ ซึ่งจะช่วยลดการสั่นพ้องของระบบเช่นกัน อย่างไรก็ตาม คุณสมบัติการลดทอนของตัวกรองจะลดลงที่ความถี่สูง รูปที่ 8 แสดงกราฟอิมพีแดนซ์เทียบกับความถี่ของ MPZ1608S101A ทั้งแบบมีและไม่มีตัวต้านทานแบบขนาน 10 Ω กราฟเส้นประสีเขียวอ่อนคืออิมพีแดนซ์โดยรวมของบีดที่ต่อตัวต้านทาน 10 Ω แบบขนาน อิมพีแดนซ์ของบีดและตัวต้านทานแบบขนานลดลงอย่างมากและถูกครอบงำโดยตัวต้านทาน 10 Ω อย่างไรก็ตาม ความถี่ครอสโอเวอร์ 3.8 MHz สำหรับบีดที่มีตัวต้านทานแบบขนาน 10 Ω นั้นต่ำกว่าความถี่ครอสโอเวอร์ของบีดเพียงตัวเดียวที่ 40.3 MHz มาก ลูกปัดดังกล่าวปรากฏเป็นตัวต้านทานที่ช่วงความถี่ที่ต่ำกว่ามาก โดยลด Q ลงเพื่อประสิทธิภาพการลดทอนที่ดีขึ้น

วิธี C ประกอบด้วยการเพิ่มตัวเก็บประจุขนาดใหญ่ (CDAMP) พร้อมตัวต้านทานการหน่วงแบบอนุกรม (RDAMP) ซึ่งมักจะเป็นวิธีแก้ปัญหาที่ดีที่สุด

การเพิ่มตัวเก็บประจุและตัวต้านทานจะช่วยลดแรงสะท้อนของระบบและไม่ลดประสิทธิภาพการบายพาสที่ความถี่สูง การนำวิธีนี้มาใช้จะช่วยป้องกันการสูญเสียพลังงานที่มากเกินไปบนตัวต้านทานเนื่องจากตัวเก็บประจุบล็อกกระแสตรงขนาดใหญ่ ตัวเก็บประจุต้องมีขนาดใหญ่กว่าผลรวมของตัวเก็บประจุแยกตัวทั้งหมด ซึ่งจะลดค่าตัวต้านทานหน่วงที่ต้องการ อิมพีแดนซ์ของตัวเก็บประจุต้องน้อยกว่าความต้านทานหน่วงที่ความถี่เรโซแนนซ์มากพอเพื่อลดจุดสูงสุด

รูปที่ 9 แสดงกราฟสเปกตรัมเอาต์พุตบวกของ ADP5071 ที่มีการหน่วงสัญญาณ Method C บนวงจรประยุกต์ใช้งานดังแสดงในรูปที่ 5 CDAMP และ RDAMP ที่ใช้คือตัวเก็บประจุเซรามิก 1 µF และตัวต้านทาน SMD 2 Ω ตามลำดับ ริปเปิลพื้นฐานที่ความถี่ 2.4 MHz ลดลง 5 dB เมื่อเทียบกับค่าเกน 10 dB ดังแสดงในรูปที่ 9

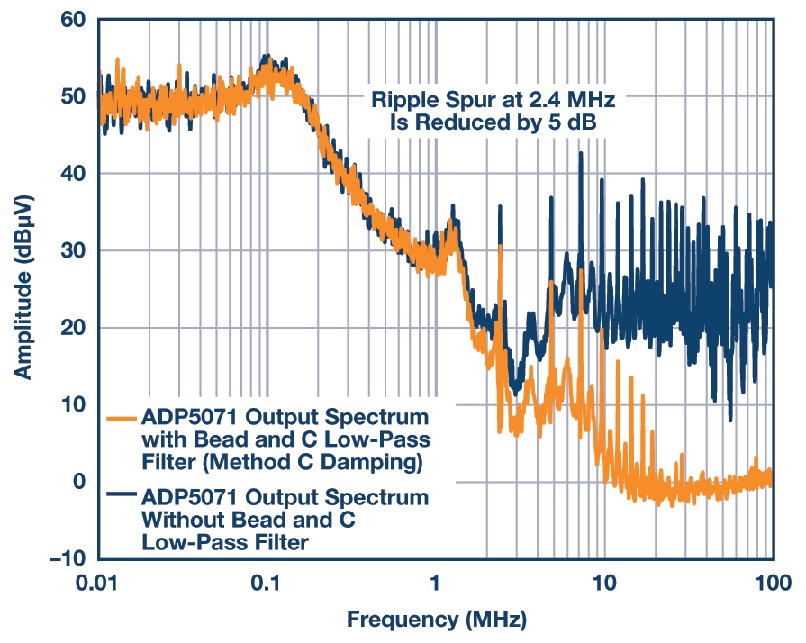
โดยทั่วไป วิธี C เป็นวิธีที่หรูหราที่สุด โดยใช้วิธีการเพิ่มตัวต้านทานแบบอนุกรมกับตัวเก็บประจุเซรามิก แทนที่จะซื้อตัวเก็บประจุแบบหน่วงเฉพาะที่มีราคาแพง การออกแบบที่ปลอดภัยที่สุดมักจะมีตัวต้านทานที่สามารถปรับแต่งได้ระหว่างการสร้างต้นแบบ และสามารถตัดออกได้หากไม่จำเป็น ข้อเสียเพียงอย่างเดียวคือต้นทุนส่วนประกอบที่เพิ่มขึ้นและพื้นที่บอร์ดที่ต้องใช้มากขึ้น

บทสรุป

บทความนี้แสดงข้อควรพิจารณาสำคัญที่ต้องพิจารณาเมื่อใช้ลูกปัดเฟอร์ไรต์ นอกจากนี้ยังมีรายละเอียดเกี่ยวกับแบบจำลองวงจรอย่างง่ายที่แสดงลูกปัด ผลการจำลองแสดงให้เห็นถึงความสัมพันธ์ที่ดีระหว่างค่าอิมพีแดนซ์ที่วัดได้จริงกับการตอบสนองความถี่ที่กระแสไบอัสศูนย์กระแสตรง

บทความนี้ยังกล่าวถึงผลกระทบของกระแสไบอัส DC ต่อคุณลักษณะของบีดเฟอร์ไรต์ แสดงให้เห็นว่ากระแสไบอัส DC ที่มากกว่า 20% ของกระแสที่กำหนดอาจทำให้ค่าความเหนี่ยวนำของบีดลดลงอย่างมีนัยสำคัญ กระแสดังกล่าวยังสามารถลดอิมพีแดนซ์ประสิทธิผลของบีดและลดความสามารถในการกรอง EMI ได้อีกด้วย เมื่อใช้บีดเฟอร์ไรต์ในรางจ่ายไฟที่มีกระแสไบอัส DC ควรตรวจสอบให้แน่ใจว่ากระแสไม่ทำให้วัสดุเฟอร์ไรต์อิ่มตัวและทำให้เกิดการเปลี่ยนแปลงค่าความเหนี่ยวนำอย่างมีนัยสำคัญ

เนื่องจากเม็ดเฟอร์ไรต์เป็นตัวนำไฟฟ้าเหนี่ยวนำ จึงไม่ควรใช้เม็ดเฟอร์ไรต์ร่วมกับตัวเก็บประจุแยกตัว Q สูงโดยไม่ระมัดระวัง การทำเช่นนี้อาจก่อให้เกิดผลเสียมากกว่าผลดี โดยทำให้เกิดการสั่นพ้องที่ไม่พึงประสงค์ในวงจร อย่างไรก็ตาม วิธีการหน่วงสัญญาณที่เสนอในบทความนี้เป็นวิธีแก้ปัญหาที่ง่ายโดยใช้ตัวเก็บประจุแยกตัวขนาดใหญ่ต่ออนุกรมกับตัวต้านทานหน่วงสัญญาณคร่อมโหลด ซึ่งจะช่วยหลีกเลี่ยงการสั่นพ้องที่ไม่พึงประสงค์ การใช้เม็ดเฟอร์ไรต์อย่างถูกต้องเป็นวิธีที่มีประสิทธิภาพและประหยัดในการลดสัญญาณรบกวนความถี่สูงและสัญญาณทรานเซียนท์แบบสวิตชิ่ง