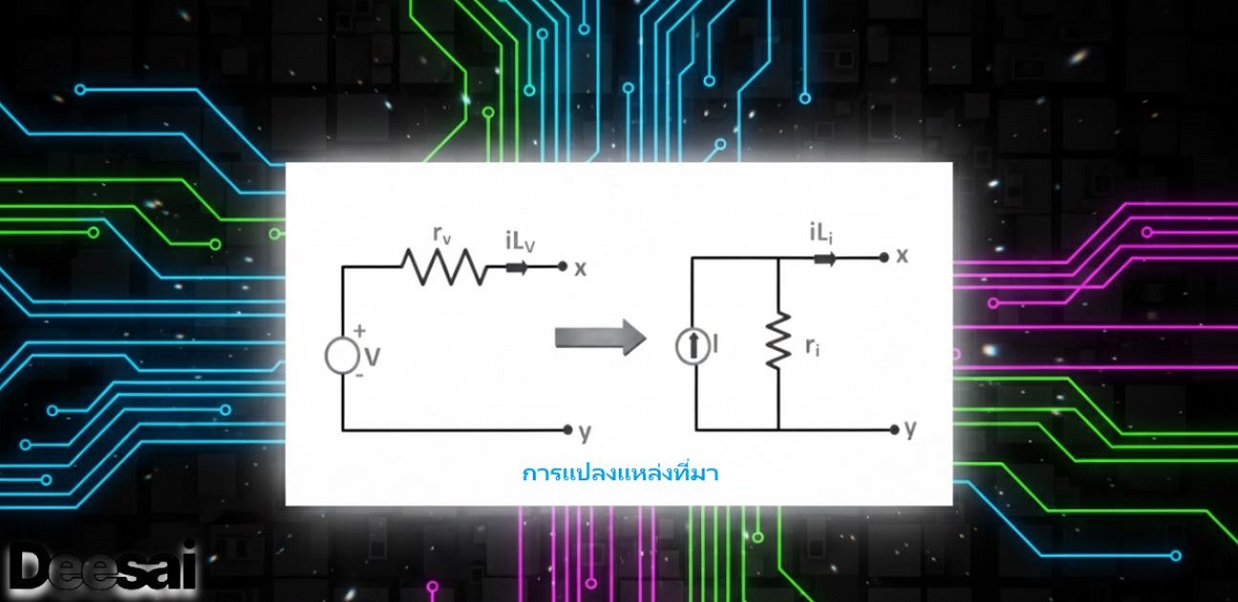
คำจำกัดความการแปลงแหล่งกำเนิด

การแปลงแหล่งกำเนิดเป็นเทคนิคสำคัญในการวิเคราะห์วงจรไฟฟ้า ซึ่งช่วยให้สามารถแปลงแรงดันไฟฟ้าระหว่างแหล่งกำเนิดแบบอนุกรมที่มีอิมพีแดนซ์และแหล่งกำเนิดกระแสแบบขนานที่มีอิมพีแดนซ์เท่ากัน และในทางกลับกัน วิธีนี้ใช้ได้กับทั้งแหล่งกำเนิดอิสระและแหล่งกำเนิดอิสระ โดยต้องพิจารณาอย่างรอบคอบสำหรับแหล่งกำเนิดอิสระ

กระบวนการนี้ขึ้นอยู่กับกฎของโอห์ม ซึ่งระบุว่า:

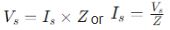
หรือ V_s  คือ แหล่ง จ่ายแรงดันไฟฟ้า I_s คือแหล่งจ่ายกระแสไฟฟ้า และ ? คืออิมพีแดนซ์

ในการแปลงแหล่งจ่ายแรงดันเป็นแหล่งจ่ายกระแส ให้ใช้:

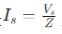
หลังจากคำนวณ I_s แล้ว ให้วาดโครงร่างของแหล่งจ่ายแรงดันเดิมใหม่ โดยแทนที่ด้วย ? และต่อขนาน ในทางกลับกัน ในการแปลงแหล่งจ่ายกระแสเป็นแหล่งจ่ายแรงดัน ให้ใช้: V₈=I_s x Z จากนั้นกำหนดค่าวงจรใหม่ด้วย V_s sin อนุกรมกับ? เทคนิคนี้ช่วยลดความซับซ้อนของการวิเคราะห์วงจรที่ซับซ้อน โดยทำให้การตรวจสอบความต้านทานแบบอนุกรมและขนานง่ายขึ้น โดยยังคงรักษาความสัมพันธ์ระหว่างแรงดันและกระแสไว้ ทำให้มั่นใจได้ว่าทั้งวงจรที่แปลงแล้วและวงจรเดิมมีพฤติกรรมที่เท่าเทียมกัน การนำเสนอวงจรแบบง่ายทำให้การใช้กฎของเคอร์ชอฟฟ์และวิธีการวิเคราะห์อื่นๆ ง่ายขึ้น

ฟอร์มเทเวนิน

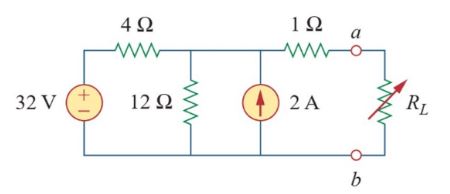
ทฤษฎีบทของเทเวแนงลดวงจรเชิงเส้นที่มีแหล่งจ่ายแรงดัน กระแส และความต้านทาน ให้เหลือเพียงแหล่งจ่ายแรงดันเดียวและความต้านทานแบบอนุกรม ซึ่งเกี่ยวข้องกับการระบุโหนดสองโหนดและแบ่งวงจรออกเป็นส่วนๆ ที่จัดการได้

ในการหาค่าแรงดันไฟฟ้าสมมูล ( V_oc ) ให้แยกส่วนของวงจรที่สนใจและวัดแรงดันไฟฟ้าคร่อมโหนด ความต้านทานสมมูล ( R_TH ) คำนวณได้จากการปิดแหล่งจ่ายอิสระทั้งหมด โดยแปลงแหล่งจ่ายแรงดันไฟฟ้าเป็นไฟฟ้าลัดวงจร และแปลงแหล่งจ่ายกระแสเป็นไฟฟ้าเปิด และวัดค่าความต้านทานระหว่างโหนด ผลลัพธ์ที่ได้คือวงจรสมมูลเทเวนิน: แหล่งจ่ายแรงดันไฟฟ้า ( V_T ) ต่ออนุกรมกับความต้านทาน ( R_T )

หากต้องการแปลงสิ่งนี้ให้เทียบเท่ากับ Norton ให้ใช้:

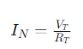
มีประสิทธิผลในการใช้สำหรับ:

โครงข่ายไฟฟ้า - โครงข่ายไฟฟ้าจ่ายไฟฟ้าให้กับบ้านเรือนและอุตสาหกรรมผ่านเครือข่ายสายส่งและอุปกรณ์สถานีย่อยที่ซับซ้อน วิศวกรใช้ทฤษฎีบทของเทเวนิน (Thevenin's Theorem) เพื่อจำลองโครงข่ายไฟฟ้าเหล่านี้ โดยทำให้วงจรเหล่านี้เรียบง่ายลงเป็นวงจรสมมูล แบบจำลองนี้ช่วยในการวิเคราะห์การไหลของไฟฟ้า แรงดันไฟฟ้าตก และเสถียรภาพโดยรวมของระบบ

อุปกรณ์อิเล็กทรอนิกส์ - ทฤษฎีบทของเทเวนินมีประโยชน์ในการออกแบบและวิเคราะห์อุปกรณ์อิเล็กทรอนิกส์ เช่น สมาร์ทโฟน คอมพิวเตอร์ และระบบเสียง ทฤษฎีบทนี้ช่วยให้วิศวกรสามารถลดความซับซ้อนของวงจรให้เทียบเท่ากัน ทำให้เข้าใจและคาดการณ์พฤติกรรมของอุปกรณ์ภายใต้สภาวะต่างๆ ได้ง่ายขึ้น การลดความซับซ้อนนี้เป็นกุญแจสำคัญในการแก้ไขปัญหาแรงดันไฟฟ้าตกบนเมนบอร์ดคอมพิวเตอร์และการสร้างแหล่งจ่ายไฟที่มีประสิทธิภาพ ซึ่งเน้นย้ำถึงบทบาทสำคัญของทฤษฎีบทนี้ในการเพิ่มประสิทธิภาพทางอิเล็กทรอนิกส์

การแก้ไขปัญหาวงจร - ทฤษฎีบทของเทเวนินช่วยลดความยุ่งยากของงานนี้โดยช่วยให้วิศวกรและช่างเทคนิคสามารถแทนที่ส่วนวงจรที่ซับซ้อนด้วยค่าเทียบเท่าที่เรียบง่ายกว่าได้ วิธีนี้ช่วยแยกและวิเคราะห์ส่วนประกอบหรือส่วนวงจรแต่ละส่วน ทำให้ระบุและแก้ไขข้อผิดพลาดได้ง่ายขึ้น

นอร์ตันฟอร์ม

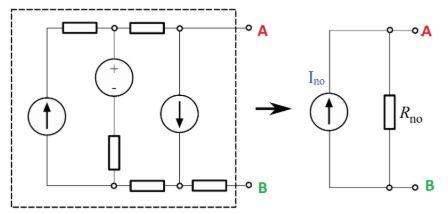
ทฤษฎีบทของนอร์ตันเสริมทฤษฎีบทของเทเวแน็งด้วย การแปลงเครือข่ายความต้านทานและแหล่งจ่ายกระแสไฟฟ้าให้เป็นแหล่งจ่ายกระแสไฟฟ้าเดียวขนานกับความต้านทานเพียงตัวเดียว ตัวชี้วัดสำคัญคือกระแสไฟฟ้าลัดวงจร ( I_sc ) ที่ขั้วของเครือข่าย ซึ่งหาได้จากการลัดวงจรขั้วเอาต์พุตและการวัดกระแสไฟฟ้า

ระบุโหนดสำคัญสองโหนดเพื่อวิเคราะห์แต่ละส่วนของวงจรแยกกัน หากไม่มีแหล่งที่มาที่ขึ้นต่อกัน หรือหากผลกระทบของแหล่งที่มาเหล่านั้นมีอยู่ในส่วนของแต่ละส่วน สมการเทียบเท่านอร์ตันจะถูกจำลองโดยการคำนวณ Iscและความต้านทานแบบขนาน ( R_N ) ซึ่งหาได้จากการกำหนดค่าศูนย์ให้กับแหล่งที่มาทั้งหมดในส่วนนั้น แบบฟอร์มนี้ช่วยลดความซับซ้อนของการวิเคราะห์วงจร ซึ่งการแปลงกลับเป็นรูปแบบเทเวนินประกอบด้วย:

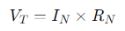
ค่าความต้านทานในทั้งสองรูปแบบเท่ากัน:

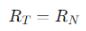
ทฤษฎีบทของนอร์ตันใช้ได้ผลดีสำหรับ:

การแทนที่ส่วนเครือข่ายขนาดใหญ่ด้วยวงจรอย่างง่าย - ทฤษฎีบทของนอร์ตัน ช่วยให้วิศวกรสามารถแทนที่ส่วนสำคัญของเครือข่ายไฟฟ้าด้วยวงจรสมมูลซึ่งประกอบด้วยแหล่งจ่ายกระแสไฟฟ้าเพียงตัวเดียวขนานกับตัวต้านทานเพียงตัวเดียว การลดความซับซ้อนนี้มีประโยชน์อย่างยิ่งในการวิเคราะห์ระบบไฟฟ้าและเครือข่ายไฟฟ้าขนาดใหญ่อื่นๆ ที่การจัดการส่วนประกอบแต่ละส่วนแยกกันไม่สามารถทำได้ในทางปฏิบัติ

การลดความซับซ้อนของการวิเคราะห์เครือข่าย - ทฤษฎีบทของนอร์ตัน สามารถลดความซับซ้อนของการวิเคราะห์วงจรที่ซับซ้อนโดยมุ่งเน้นไปที่กระแส ซึ่งมีประโยชน์อย่างยิ่งในสถานการณ์ที่การวิเคราะห์กระแสให้ข้อมูลเชิงลึกเกี่ยวกับประสิทธิภาพของวงจรโดยตรงมากขึ้น เช่น การวิเคราะห์การลัดวงจร หรือการศึกษาวงจรที่มีสาขาขนานหลายสาขา โดยการแปลงแหล่งจ่ายแรงดันไฟฟ้าและตัวต้านทานแบบตาข่ายที่ซับซ้อนให้เป็นแบบจำลองที่ง่ายขึ้นด้วยแหล่งจ่ายกระแสไฟฟ้าเพียงตัวเดียวและตัวต้านทานแบบขนาน

การถ่ายโอนกำลังไฟฟ้าสูงสุด - ตามทฤษฎีบทการถ่ายโอนกำลังไฟฟ้าสูงสุด กำลังไฟฟ้าสูงสุดจะถูกถ่ายโอนไปยังโหลดเมื่อความต้านทานของโหลดเท่ากับความต้านทานภายในของแหล่งกำเนิดไฟฟ้าเมื่อมองจากมุมมองของโหลด ด้วยทฤษฎีบทของนอร์ตัน ความต้านทานของแหล่งกำเนิดไฟฟ้าสามารถหาค่าได้อย่างง่ายดายโดยใช้ความต้านทานของวงจรสมมูลของนอร์ตัน การลดความซับซ้อนนี้มีประโยชน์อย่างมากในระบบสื่อสาร เครือข่ายจ่ายไฟฟ้า และระบบขยายเสียง

การวิเคราะห์วงจรเชิงคำนวณ - วงจรอิเล็กทรอนิกส์มักใช้ทฤษฎีบทของนอร์ตันเพื่อเพิ่มประสิทธิภาพในการคำนวณ ด้วยการลดความซับซ้อนของเครือข่ายให้เหลือเพียงค่าเทียบเท่าที่เรียบง่าย เครื่องมือเหล่านี้จึงสามารถจำลองสถานการณ์ได้เร็วขึ้นและมีค่าใช้จ่ายในการคำนวณน้อยลง

การแปลงแหล่งจ่ายแรงดันไฟฟ้า

เริ่มต้นด้วยวงจรง่ายๆ: แหล่งจ่ายแรงดันและตัวต้านทานแบบอนุกรม โดยใช้กฎของโอห์ม ( I=V/R ) คุณสามารถเปลี่ยนรูปแบบวงจรนี้ให้เป็นวงจรแบบขนาน โดยที่ตัวต้านทานยังคงเท่าเดิม แต่แหล่งจ่ายจะเปลี่ยนจากแรงดันเป็นกระแส

ตัวอย่างเช่น ลองพิจารณาแหล่งจ่ายแรงดันไฟฟ้า 10V ที่ต่อแบบอนุกรมกับตัวต้านทาน 2Ω เพื่อทำการแปลง ให้คำนวณค่าเทียบเท่าของแหล่งจ่ายกระแสโดยใช้:

ผลลัพธ์ที่ได้คือวงจรใหม่ที่มีแหล่งจ่ายกระแส 5A ขนานกับตัวต้านทาน 2Ω การแปลงนี้ช่วยลดความยุ่งยากในการวิเคราะห์วงจรโดยการรักษาค่าส่วนประกอบให้คงที่ พร้อมกับเปลี่ยนการกำหนดค่าเพื่อให้ตรวจสอบได้ง่ายขึ้น

เครื่องคำนวณการแปลงแหล่งจ่ายแรงดันไฟฟ้า

เครื่องคำนวณการแปลงแหล่งจ่ายแรงดันไฟฟ้าเป็นเครื่องมือที่มีประโยชน์สำหรับการแปลงวงจรอนุกรมที่มีแหล่งจ่ายแรงดันไฟฟ้าและตัวต้านทานให้เป็นแหล่งจ่ายกระแสไฟฟ้าขนานเทียบเท่า ในการใช้เครื่องมือนี้ ให้ป้อนค่าแรงดันไฟฟ้าและความต้านทาน จากนั้นเครื่องคำนวณจะใช้กฎของโอห์มเพื่อคำนวณกระแสในวงจรที่แปลงแล้ว โดยยังคงค่าความต้านทานเดิมไว้

เครื่องมือนี้ช่วยวิเคราะห์การแปลงวงจร ทำให้หลักการทางไฟฟ้าใช้งานได้จริงมากขึ้น มีประโยชน์อย่างยิ่งในวิศวกรรมไฟฟ้าสำหรับการปรับปรุงกระบวนการออกแบบและการแก้ไขปัญหา

การแปลงแหล่งกำเนิดกระแสไฟฟ้า

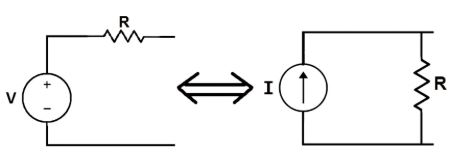
ลองพิจารณาตัวอย่างการใช้งานจริง: แหล่งจ่ายกระแส 2A ต่อขนานกับตัวต้านทาน 3Ω โดยการใช้สูตร เราสามารถคำนวณแหล่งจ่ายแรงดันไฟฟ้าเทียบเท่าได้ดังนี้

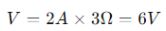
ผลลัพธ์ที่ได้คือวงจรที่ถูกแปลงแล้ว โดยมีแหล่งจ่ายแรงดัน 6V ต่ออนุกรมกับตัวต้านทาน 3Ω ตัวเดียวกัน วิธีการเชิงระบบนี้ช่วยวิเคราะห์และทำความเข้าใจพฤติกรรมของวงจรภายใต้การกำหนดค่าที่แตกต่างกัน พร้อมทั้งรับประกันว่าพฤติกรรมของโหลดยังคงสอดคล้องกันตลอดกระบวนการแปลง

เครื่องคำนวณการแปลงแหล่งกำเนิดกระแสไฟฟ้า

เครื่องคำนวณการแปลงแหล่งจ่ายกระแสเป็นเครื่องมือที่มีประโยชน์สำหรับการแปลงวงจรขนานที่มีแหล่งจ่ายกระแสและตัวต้านทานให้เป็นรูปแบบแหล่งจ่ายแรงดันไฟฟ้าแบบอนุกรมสมมูล ผู้ใช้ป้อนค่ากระแสและความต้านทาน จากนั้นเครื่องคำนวณจะใช้สูตร V = I × R เพื่อหาค่าแรงดันไฟฟ้าสมมูล

เครื่องมือนี้สาธิตการประยุกต์ใช้หลักการไฟฟ้าในทางปฏิบัติ ช่วยให้วิศวกรและนักศึกษาเห็นภาพและดำเนินการแปลงวงจรได้อย่างแม่นยำ ช่วยลดความซับซ้อนของกระบวนการออกแบบและเพิ่มประสิทธิภาพการสาธิตทางการศึกษา ทำให้เป็นแหล่งข้อมูลสำคัญทั้งในเชิงวิชาการและวิชาชีพ

การแปลงแหล่งกำเนิดไฟฟ้ากระแสสลับ

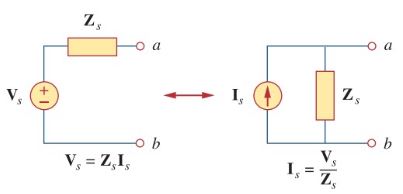
การแปลงแหล่งจ่ายไฟฟ้ากระแสสลับ (AC) ใช้ได้กับวงจรที่มีตัวเก็บประจุและตัวเหนี่ยวนำ ไม่ใช่แค่วงจรต้านทานเท่านั้น เทคนิคนี้ใช้หลักการจากทฤษฎีบทของเทเวแน็งและนอร์ตัน เพื่อปรับแหล่งจ่ายไฟฟ้ากระแสสลับและอิมพีแดนซ์ที่เกี่ยวข้อง เพื่อให้แน่ใจว่าความสัมพันธ์ของโดเมนความถี่ยังคงสอดคล้องกัน

ขั้นแรก ให้วิเคราะห์แหล่งจ่ายไฟฟ้ากระแสสลับ (AC) เสมือนเป็นแหล่งจ่ายไฟฟ้ากระแสตรง (DC) เพื่อกำหนดค่าแรงดันหรือกระแสพื้นฐาน ขั้นตอนนี้จะเป็นพื้นฐานสำหรับการคำนวณเพิ่มเติมในบริบทของแหล่งจ่ายไฟฟ้ากระแสสลับ ขั้นต่อไป ให้พิจารณาคุณลักษณะที่ขึ้นอยู่กับความถี่ของตัวเก็บประจุและตัวเหนี่ยวนำโดยการคำนวณค่าอิมพีแดนซ์ใหม่ที่ความถี่การทำงานของวงจร ใช้สูตรต่อไปนี้:

สำหรับตัวเก็บประจุ:

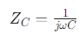
สำหรับตัวเหนี่ยวนำ:

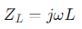
ที่ไหน ? คือความถี่เชิงมุม

การนำค่าอิมพีแดนซ์ที่คำนวณได้มาใช้ในบริบทของการแปลงแหล่งจ่ายไฟฟ้ากระแสสลับ (AC) เป็นขั้นตอนสำคัญในการสร้างแบบจำลองและทำความเข้าใจพฤติกรรมของวงจรอย่างแม่นยำภายใต้สภาวะการทำงานต่างๆ กระบวนการนี้เกี่ยวข้องกับการปรับแหล่งจ่ายไฟฟ้ากระแสสลับภายในวงจรให้สะท้อนการเปลี่ยนแปลงค่าอิมพีแดนซ์ ซึ่งอาจผันผวนเนื่องจากปัจจัยต่างๆ เช่น การเปลี่ยนแปลงความถี่หรือการเปลี่ยนแปลงส่วนประกอบ

ความสำคัญของวิธีนี้ขยายไปสู่การประยุกต์ใช้ในทางปฏิบัติที่หลากหลาย โดยเฉพาะอย่างยิ่งในสาขาการตอบสนองความถี่และพฤติกรรมไดนามิก ในระบบประมวลผลสัญญาณและระบบสื่อสาร พฤติกรรมไดนามิกที่สม่ำเสมอจะถูกรักษาไว้ด้วยการแปลงพลังงานไฟฟ้ากระแสสลับที่แม่นยำ ซึ่งทำให้มั่นใจได้ว่าระบบจะสามารถรองรับความถี่สัญญาณที่เปลี่ยนแปลงได้โดยไม่สูญเสียฟังก์ชันการทำงาน

การแปลงแหล่งจ่ายไฟ AC เป็นสิ่งจำเป็นอย่างยิ่งสำหรับการออกแบบและการแก้ไขปัญหาวงจร วิธีการนี้ช่วยให้วิศวกรสามารถจำลองและคาดการณ์การตอบสนองของวงจรต่อสภาวะต่างๆ ได้อย่างลึกซึ้งยิ่งขึ้น ซึ่งช่วยให้เข้าใจวงจร AC ได้อย่างลึกซึ้งยิ่งขึ้น นอกจากนี้ยังช่วยให้สามารถบริหารจัดการและเพิ่มประสิทธิภาพของระบบเหล่านี้ได้อย่างมีประสิทธิภาพมากขึ้น เพื่อให้มั่นใจว่าระบบทำงานตามข้อกำหนดที่ต้องการ

การแปลงแรงดันไฟฟ้าเป็นกระแสไฟฟ้า

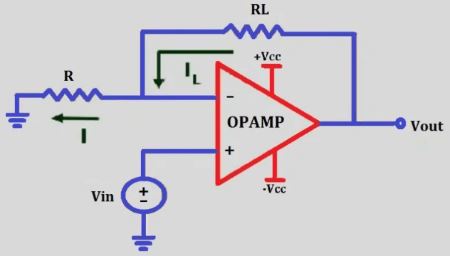
กระบวนการแปลงแรงดันไฟฟ้าเป็นกระแสไฟฟ้าประกอบด้วยขั้นตอนสำคัญหลายขั้นตอนเพื่อให้มั่นใจถึงความแม่นยำและประสิทธิภาพ แหล่งจ่ายแรงดันไฟฟ้าต้องลัดวงจรโดยการต่อขั้วโดยตรง การกระทำนี้จะสร้างเส้นทางการไหลของกระแสไฟฟ้า ซึ่งต่อมาจะผ่านตัวต้านทานที่มีค่าความต้านทานเท่ากับค่าความต้านทานเดิม เพื่อรักษาความสมบูรณ์ของวงจร แหล่งจ่ายกระแสไฟฟ้าต้องอยู่ในตำแหน่งที่ถูกต้องเพื่อให้แน่ใจว่าชี้ไปยังขั้วบวกของแหล่งจ่ายแรงดันไฟฟ้าที่วางไว้ก่อนหน้านี้

เพื่อเพิ่มความแม่นยำในการแปลงแรงดันไฟฟ้าเป็นกระแส จึงมีการใช้ออปแอมป์ (op-amp) ออปแอมป์อย่าง LM741 นำเสนอการควบคุมกระแสโดยอิงตามระดับแรงดันไฟฟ้าขาเข้า จึงมีกลไกการควบคุมที่แม่นยำสูง การกำหนดค่าวงจรออปแอมป์เกี่ยวข้องกับการเลือกแบบจำลองออปแอมป์ที่เหมาะสมและการออกแบบวงจรให้รองรับโหลดแบบลอยตัวหรือแบบกราวด์ กลไกป้อนกลับที่ติดตั้งในวงจรจะปรับกระแสแบบไดนามิกตามการเปลี่ยนแปลงของโหลด ความสามารถในการปรับตัวนี้เกิดขึ้นได้จากการใช้อุปกรณ์เซมิคอนดักเตอร์ ซึ่งเป็นส่วนสำคัญในการออกแบบวงจรสมัยใหม่

การแปลงกระแสเป็นแรงดันไฟฟ้า

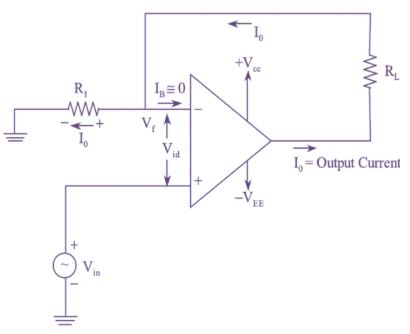
การแปลงกระแสเป็นแรงดันโดยใช้ออปแอมป์ (op-amp) เกี่ยวข้องกับแนวทางที่มีโครงสร้างเพื่อให้ได้ทั้งความเป็นเชิงเส้นและความแม่นยำ ขั้นตอนแรกของกระบวนการแปลงนี้จำเป็นต้องเลือกออปแอมป์ที่เหมาะสมและตรงตามข้อกำหนดเฉพาะของการใช้งาน เมื่อเลือกแล้ว กระแสอินพุตจะถูกป้อนเข้าสู่วงจรออปแอมป์ การตั้งค่านี้จำเป็นเนื่องจากมีผลต่อประสิทธิภาพของออปแอมป์ในการประมวลผลกระแสขาเข้า ขั้นตอนที่สามคือการกำหนดค่าวงจรเพื่อปรับกระแสให้เป็นแรงดันเอาต์พุตตามสัดส่วน

ออปแอมป์มีประโยชน์อย่างยิ่งในการใช้งาน เช่น เซ็นเซอร์โฟโตไดโอด ซึ่งความเข้มของแสงมีผลโดยตรงต่อกระแสเอาต์พุต ในสถานการณ์เช่นนี้ ออปแอมป์มีบทบาทสำคัญโดยการแปลงกระแสที่เปลี่ยนแปลงให้เป็นแรงดันเอาต์พุตที่เสถียรอย่างแม่นยำ ช่วยรักษาความสมบูรณ์ของสัญญาณ ความสามารถนี้ทำให้ออปแอมป์เป็นส่วนประกอบที่ขาดไม่ได้ในอุปกรณ์วัดความแม่นยำที่ต้องการรักษาความแม่นยำในการแปลงสัญญาณ

การลดความซับซ้อนของวงจร

การแปลงแหล่งกำเนิดเป็นวิธีที่มีประสิทธิภาพในการลดความซับซ้อนของวงจรที่ซับซ้อนโดยการแปลงระหว่างแหล่งกำเนิดแรงดันและกระแสไฟฟ้า เทคนิคนี้ช่วยรักษาคุณสมบัติทางไฟฟ้าของวงจรไว้ พร้อมทั้งทำให้เข้าใจ ออกแบบ และแก้ไขปัญหาได้ง่ายขึ้น

กระบวนการแปลงแหล่งกำเนิดไฟฟ้าในวิศวกรรมไฟฟ้าประกอบด้วยขั้นตอนที่มีโครงสร้างหลายขั้นตอน ซึ่งอำนวยความสะดวกในการทำให้แผนภาพวงจรง่ายขึ้น จึงช่วยเพิ่มทั้งความแม่นยำและความรวดเร็วในการวิเคราะห์วงจร ขั้นตอนแรกของกระบวนการนี้คือการระบุชนิดของแหล่งกำเนิดไฟฟ้าที่เกี่ยวข้อง ไม่ว่าจะเป็นแหล่งกำเนิดแรงดันไฟฟ้าหรือแหล่งกำเนิดกระแสไฟฟ้า เมื่อได้ชนิดของแหล่งกำเนิดไฟฟ้าแล้ว ขั้นตอนต่อไปคือการใช้สูตรการแปลงที่เหมาะสมเพื่อแปลงแหล่งกำเนิดแรงดันไฟฟ้าเป็นแหล่งกระแสไฟฟ้า หรือในทางกลับกัน การปรับเปลี่ยนทางคณิตศาสตร์นี้ยึดตามหลักการทางไฟฟ้าที่ได้รับการยอมรับ และช่วยให้สามารถแลกเปลี่ยนระหว่างแหล่งกำเนิดไฟฟ้าทั้งสองประเภทนี้ได้อย่างราบรื่นตามความต้องการในการวิเคราะห์ หลังจากแปลงแหล่งกำเนิดไฟฟ้าแล้ว จะต้องวาดแผนภาพวงจรใหม่เพื่อให้สะท้อนถึงแหล่งกำเนิดไฟฟ้าที่แปลงแล้วได้อย่างแม่นยำ

แบบจำลองที่สมจริงสำหรับแหล่งที่มา

แม้ว่าแบบจำลองแหล่งจ่ายแรงดันและกระแสในอุดมคติจะเป็นพื้นฐานทางวิศวกรรมไฟฟ้า แต่แบบจำลองที่ใช้งานได้จริงจะรวมเอาค่าความต้านทานภายในที่มีผลกระทบอย่างมีนัยสำคัญต่อพฤติกรรมของแหล่งจ่ายภายใต้สภาวะการใช้งานจริง ความต้านทานภายในเหล่านี้สามารถทำนายประสิทธิภาพของวงจรในโลกแห่งความเป็นจริงได้อย่างแม่นยำ ความต้านทานเหล่านี้ส่งผลต่อพฤติกรรมของแหล่งจ่ายไฟภายใต้สภาวะโหลดที่แตกต่างกัน ทำให้สามารถประเมินลักษณะการทำงานที่แท้จริงของวงจรได้

การนำแบบจำลองเชิงปฏิบัติจริงที่มีความต้านทานภายในมาประยุกต์ใช้เป็นส่วนหนึ่งของกรอบแนวคิดทางทฤษฎีเป็นสิ่งจำเป็นอย่างยิ่งในการเชื่อมช่องว่างระหว่างแนวคิดในตำราเรียนและการประยุกต์ใช้จริง แนวทางนี้ไม่เพียงแต่ช่วยเพิ่มความน่าเชื่อถือของแบบจำลองเชิงทฤษฎีเท่านั้น แต่ยังช่วยให้แบบจำลองสามารถนำไปประยุกต์ใช้และสะท้อนสถานการณ์จริงได้ดียิ่งขึ้น การนำข้อจำกัดเชิงปฏิบัติเหล่านี้มาบูรณาการจะช่วยให้วิศวกรมีความเข้าใจที่ลึกซึ้งยิ่งขึ้นเกี่ยวกับการทำงานของวงจรในการใช้งานจริง ซึ่งจะทำให้มั่นใจได้ว่าการออกแบบและกลยุทธ์การแก้ปัญหาจะมีประสิทธิภาพและสอดคล้องกับบริบทของอิเล็กทรอนิกส์สมัยใหม่

ความเท่าเทียมกันของแหล่งที่มา

แนวคิดเรื่องความเท่าเทียมของแหล่งกำเนิดไฟฟ้ามีความสำคัญอย่างยิ่งยวดในวิศวกรรมไฟฟ้า เนื่องจากมีบทบาทสำคัญอย่างยิ่งต่อการสร้างความสม่ำเสมอของพฤติกรรมทางไฟฟ้าและการเพิ่มความน่าเชื่อถือของการวิเคราะห์วงจร วิศวกรสามารถมั่นใจได้ว่าวงจรจะทำงานได้เหมือนกันทุกประการ โดยการรักษาความต้านทานภายในให้เท่ากันเมื่อเปลี่ยนแหล่งกำเนิดไฟฟ้าชนิดหนึ่งเป็นอีกชนิดหนึ่ง ไม่ว่าจะใช้แหล่งกำเนิดไฟฟ้าชนิดใด ความสม่ำเสมอนี้มีความสำคัญอย่างยิ่ง เพราะช่วยป้องกันความผันแปรของประสิทธิภาพการทำงาน ซึ่งอาจทำให้การวินิจฉัยและการทำงานของวงจรมีความซับซ้อนมากขึ้น

ความเท่าเทียมกันของแหล่งจ่ายมีส่วนช่วยในการคาดการณ์ผลการวิเคราะห์วงจรได้ดีขึ้น การใช้แหล่งจ่ายที่เทียบเท่ากันช่วยให้วิศวกรสามารถคาดการณ์ผลตอบสนองของวงจรได้อย่างน่าเชื่อถือมากขึ้น ช่วยให้กระบวนการออกแบบและแก้ไขปัญหาเป็นไปอย่างตรงไปตรงมาและคาดการณ์ได้แม่นยำยิ่งขึ้น

10. บทสรุป

โดยสรุป บทความนี้นำเสนอการสำรวจอย่างละเอียดเกี่ยวกับการแปลงแหล่งกำเนิดไฟฟ้า (Source Transformation) ซึ่งเป็นเทคนิคพื้นฐานในสาขาวิศวกรรมไฟฟ้า เน้นย้ำถึงความยืดหยุ่นและบทบาทสำคัญในการปรับและวิเคราะห์วงจรไฟฟ้า การอภิปรายนี้ครอบคลุมมากกว่าแค่คำอธิบายเชิงทฤษฎี ครอบคลุมการประยุกต์ใช้จริงในระบบโครงข่ายไฟฟ้า การปรับแต่งอุปกรณ์อิเล็กทรอนิกส์ให้เหมาะสม และการวิเคราะห์วงจรเชิงคำนวณ การนำเสนอเครื่องมือต่างๆ เช่น เครื่องคำนวณการแปลงแหล่งกำเนิดไฟฟ้ากระแสสลับ (Voltage and Current Source Transformation Calculators) แสดงให้เห็นถึงความมุ่งมั่นที่จะทำให้หลักการเหล่านี้เข้าถึงและนำไปใช้ได้มากขึ้น การอภิปรายเกี่ยวกับการแปลงแหล่งกำเนิดไฟฟ้ากระแสสลับยังเน้นย้ำถึงความสามารถในการปรับใช้ของวิธีการเหล่านี้ในวงจรประเภทต่างๆ และแสดงให้เห็นถึงความสำคัญของวิธีการเหล่านี้ในการรักษาความน่าเชื่อถือและประสิทธิภาพของระบบในสภาวะการทำงานที่หลากหลาย บทความนี้เชื่อมโยงความหมายของการผสมผสานแบบจำลองที่ใช้งานได้จริงเข้ากับความต้านทานภายในอย่างชัดเจน ซึ่งจะช่วยเพิ่มความแม่นยำในการทำนายและความเกี่ยวข้องในทางปฏิบัติของแบบจำลองบริสุทธิ์ ภาพรวมที่สมบูรณ์นี้ไม่เพียงแต่พัฒนาความเข้าใจเกี่ยวกับการแปลงแหล่งกำเนิดไฟฟ้าเท่านั้น แต่ยังเน้นย้ำถึงบทบาทสำคัญของวิธีการเหล่านี้ในการพัฒนาสาขาวิศวกรรมไฟฟ้าอีกด้วย