การเรียนรู้เชิงลึกได้ปฏิวัติอุตสาหกรรมต่างๆ นำไปสู่การพัฒนาแอปพลิเคชันทางธุรกิจใหม่ๆ อย่างต่อเนื่อง อย่างไรก็ตาม เนื่องจากโมเดล AI มีความซับซ้อนมากขึ้น จึงจำเป็นต้องใช้หน่วยความจำและระบบคอมพิวเตอร์ที่ทรงพลังมากขึ้นเพื่อให้ทำงานได้อย่างมีประสิทธิภาพ

เมื่อ AI ก้าวเข้าสู่อุปกรณ์เอดจ์ ซึ่งมักมีพลังงาน หน่วยความจำ และความสามารถในการประมวลผลที่จำกัด ข้อจำกัดของเครือข่ายประสาทเทียมที่ใช้พลังงานสูงในปัจจุบันก็เริ่มปรากฏชัดขึ้นเรื่อยๆ ในทางกลับกัน การนำเครือข่ายประสาทเทียมดังกล่าวไปใช้งานในสภาพแวดล้อมคลาวด์ก็ก่อให้เกิดต้นทุนการประมวลผลที่สูง ซึ่งเป็นข้อจำกัดด้านความสามารถในการปรับขนาดและผลกำไรของบริษัท

วิธีแก้ปัญหาที่มีแนวโน้มดีสำหรับความท้าทายเหล่านี้คือ Model Quantization บทความนี้จะแนะนำแนวคิดของ Model Quantization พร้อมทั้งสำรวจประเภท เทคนิค ข้อดี ข้อเสีย และอื่นๆ อีกมากมาย

มาเริ่มต้นด้วยการทำความเข้าใจการวัดเชิงปริมาณแบบจำลองและเหตุใดจึงมีความจำเป็น

Quantization คืออะไร?

นักพัฒนาต้องลดขนาดของโมเดลโดยไม่ลดทอนความแม่นยำ เพื่อนำเครือข่ายประสาทเทียมไปใช้งานบนคลาวด์และอุปกรณ์เอดจ์ได้อย่างมีประสิทธิภาพและประสิทธิผล การทำให้โมเดลควอนไทซ์ช่วยแก้ไขปัญหาเหล่านี้ได้

หากต้องการทำความเข้าใจการหาปริมาณ คุณต้องเข้าใจประเภทข้อมูลในการเรียนรู้เชิงลึกก่อนว่าข้อมูลเหล่านั้นถูกแปลงและแสดงอย่างไรเพื่อให้ได้แบบจำลองที่มีขนาดลดลง แบบจำลองที่ถูกหาปริมาณและไม่ถูกหาปริมาณแตกต่างกันอย่างไร เป็นต้น

ประเภทข้อมูล

เครือข่ายประสาทเทียม (NN) คือเลขทศนิยมแบบจุดลอยตัวที่เก็บไว้ในหน่วยความจำของคอมพิวเตอร์ เมื่อความซับซ้อนของ NN เพิ่มขึ้น ขนาดของตัวเลขเหล่านี้ก็จะเพิ่มขึ้นตามไปด้วย ในการเรียนรู้เชิงลึก มักใช้เลขทศนิยมแบบ 32 บิต (FP32) และ 16 บิต (FP16)

รูปแบบจุดลอยตัวเฉพาะ เช่น TensorFloat (TF32) ของ NVIDIA, FP24 ของ AMD และ BrainFloat (Bfloat16) ของ Google ก็ได้รับการออกแบบมาเพื่อเพิ่มประสิทธิภาพเช่นกัน นอกจากนี้ ยังมีรูปแบบขนาดเล็กอีกหลายรูปแบบที่เรียกกันทั่วไปว่า minifloat (เช่น FP8) ซึ่งถูกนำไปใช้งานในไมโครคอนโทรลเลอร์สำหรับอุปกรณ์ฝังตัว และได้รับการรองรับโดย GPU รุ่นใหม่ เช่น H100 ของ NVIDIA

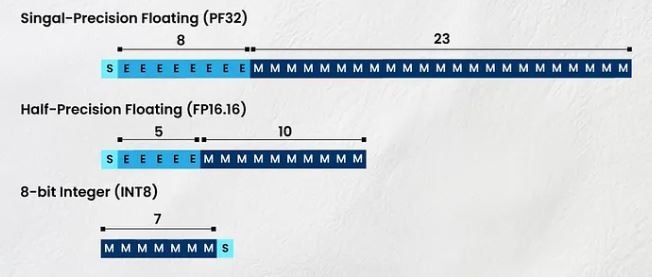
รูปแบบหรือการแสดงผลที่แตกต่างกันเหล่านี้สำหรับการจัดเก็บตัวเลขมีความสำคัญอย่างยิ่ง เนื่องจากแต่ละรูปแบบจะใช้หน่วยความจำเฉพาะส่วน ด้านล่างนี้ เราได้กล่าวถึงบิต (b) ที่จัดสรรให้กับการแสดงผล (รูปแบบ) ที่แตกต่างกัน

Float32 (FP32) : 1b สำหรับเครื่องหมาย, 8b สำหรับเลขชี้กำลัง, 23b สำหรับแมนทิสซา (เศษส่วน)

Float16 (FP16) : 1b สำหรับเครื่องหมาย, 5b สำหรับเลขชี้กำลัง, 10b สำหรับแมนทิสซา

BF16 (B คือ Google Brain) : 1b สำหรับเครื่องหมาย 8b สำหรับเลขชี้กำลัง และ 7b สำหรับแมนทิสซา

การหาปริมาณแบบจำลอง

การวัดปริมาณแบบจำลองเป็นเทคนิคที่ลดขนาดของแบบจำลองเครือข่ายประสาทเทียมเชิงลึก (NN) โดยการแปลงน้ำหนักและพารามิเตอร์อื่นๆ จากการแสดงค่าจุดลอยตัวที่มีความแม่นยำสูงไปเป็นความแม่นยำที่ต่ำกว่า

แม้ว่าแนวทางนี้จะให้ประโยชน์ เช่น ประสิทธิภาพของโมเดลที่เพิ่มขึ้น ความเร็วในการอนุมานที่ดีขึ้น ความต้องการแบนด์วิดท์หน่วยความจำที่ลดลง และการใช้แคชที่ได้รับการปรับปรุง แต่ความท้าทายหลักอยู่ที่การทำให้แน่ใจว่าการปรับปรุงเหล่านี้จะไม่กระทบต่อความแม่นยำของโมเดล

การวัดปริมาณในเครือข่ายเชิงลึก

สำหรับการเรียนรู้เชิงลึกนั้น มีทั้งแบบความแม่นยำเดี่ยวหรือเต็มความแม่นยำ, Float32 และครึ่งความแม่นยำ ซึ่งหมายถึง Float16 และ BFloat16 โดยค่าเริ่มต้น จะใช้ความแม่นยำเต็มเพื่อฝึกฝนและจัดเก็บแบบจำลองการเรียนรู้เชิงลึก และการหาปริมาณโดยทั่วไปจะดำเนินการโดยการแปลงความแม่นยำเต็มเป็นรูปแบบ INT8 ดังนั้น การแทนค่า INT8 จึงมักถูกเรียกว่า "การควอนไทซ์"

การหาปริมาณเทียบกับการไม่หาปริมาณ

อาจมีความแตกต่างอย่างมีนัยสำคัญระหว่างแบบจำลองเชิงปริมาณและแบบจำลองที่ไม่เชิงปริมาณในแง่ของขนาดหน่วยความจำ ความเร็วในการอนุมาน ประสิทธิภาพ และคุณภาพของเอาต์พุต ตัวอย่างเช่น ในขณะที่แบบจำลองที่ไม่เชิงปริมาณอาจใช้หน่วยความจำประมาณ 3 GB แต่แบบจำลองเชิงปริมาณสามารถลดขนาดนี้ลงได้ 60–70% ซึ่งช่วยลดการใช้หน่วยความจำได้อย่างมาก

ในทำนองเดียวกัน โมเดลที่ไม่ได้ถูกวัดปริมาณอาจต้องใช้เวลา 40 มิลลิวินาทีต่อการอนุมานและใช้พลังงาน 4 จูล ในขณะที่โมเดลที่ถูกวัดปริมาณสามารถทำงานเดียวกันได้ในเวลา 20 มิลลิวินาทีด้วยพลังงาน 2 จูล ซึ่งถือว่ามีประสิทธิภาพเพิ่มขึ้น 100%

อย่างไรก็ตาม ความแม่นยำอาจลดลงได้ ตัวอย่างเช่น ใน NN ที่ใช้วิชันคอมพิวเตอร์ โมเดลเชิงปริมาณอาจสร้างภาพที่มีคุณภาพภาพต่ำกว่าภาพต้นฉบับที่ไม่ได้ถูกควอนไทซ์ 8 ถึง 10%

ความท้าทายของการวัดปริมาณแบบจำลอง

การหาปริมาณมีความสำคัญอย่างยิ่งต่อการปรับปรุงโมเดลการเรียนรู้ของเครื่องให้เหมาะสมที่สุดสำหรับการใช้งานในสภาพแวดล้อมที่มีข้อจำกัดด้านทรัพยากร เช่น อุปกรณ์พกพาและการประมวลผลแบบเอจ การลดความแม่นยำของพารามิเตอร์และการดำเนินการของโมเดล การหาปริมาณสามารถลดขนาดของโมเดล ลดการใช้หน่วยความจำ และเพิ่มความเร็วในการอนุมาน อย่างไรก็ตาม อาจเกิดความท้าทายหลายประการ ได้แก่

1) ความต้องการความรู้เชิงลึก

โมเดลที่แตกต่างกันจำเป็นต้องใช้วิธีการวัดปริมาณที่แตกต่างกัน และคุณต้องมีความรู้เกี่ยวกับเทคนิคเหล่านี้เป็นอย่างดี นอกจากนี้ การวัดปริมาณที่ประสบความสำเร็จมักต้องอาศัยความรู้เกี่ยวกับสถาปัตยกรรม NN มาก่อน และต้องปรับแต่งอย่างละเอียด

2) ความแม่นยำเทียบกับประสิทธิภาพ

การรักษาสมดุลระหว่างความแม่นยำและขนาดของโมเดล โดยเฉพาะอย่างยิ่งกับรูปแบบความแม่นยำต่ำ เช่น INT8 อาจเป็นเรื่องยาก ช่วงไดนามิกที่จำกัดอาจส่งผลต่อความแม่นยำในระหว่างการแปลงจากรูปแบบที่มีความแม่นยำสูงกว่า

ตัวอย่างเช่น แม้ว่า FP16 สามารถแทนที่ FP32 ได้ด้วยการสูญเสียความแม่นยำเพียงเล็กน้อยในการอนุมาน NN เชิงลึก แต่รูปแบบช่วงไดนามิกขนาดเล็กกว่าอย่าง INT8 กลับเป็นความท้าทายที่สำคัญกว่า สิ่งสำคัญที่ต้องจำไว้คือในระหว่างการควอนไทซ์ การบีบอัดช่วงไดนามิกกว้างของ FP32 ให้เหลือเพียง 255 ค่าของ INT8 หรือแม้แต่ 15 ค่าของ INT4 ถือเป็นความท้าทายที่สำคัญ

3) เทคนิคเสริม

มีการพัฒนาเทคนิคเสริมต่างๆ สำหรับการหาปริมาณแบบจำลองเพื่อรับมือกับความท้าทายเหล่านี้ ซึ่งรวมถึงการปรับสเกล (ต่อช่องสัญญาณหรือต่อชั้น) ที่ช่วยปรับสเกลและค่าจุดศูนย์ของน้ำหนักและเทนเซอร์กระตุ้นเพื่อให้เหมาะกับรูปแบบการหาปริมาณมากขึ้น

นอกจากนี้ เทคนิคต่างๆ เช่น QAT ยังจำลองกระบวนการควอนไทซ์ระหว่างการฝึกเพื่อเตรียมแบบจำลองสำหรับควอนไทซ์ การจำลองหรือการประมาณค่าพิสัยนี้ทำได้โดยกระบวนการที่เรียกว่าการสอบเทียบ การสอบเทียบเกี่ยวข้องกับการกำหนดพารามิเตอร์หรือการปรับค่าที่เหมาะสมเพื่อให้แน่ใจว่าแบบจำลองควอนไทซ์นั้นสะท้อนพฤติกรรมของแบบจำลองความแม่นยำเต็มรูปแบบดั้งเดิมได้อย่างใกล้ชิด

กระบวนการสอบเทียบจะแตกต่างกันไปขึ้นอยู่กับประเภทของโมเดลและกรณีการใช้งาน โดยมีเทคนิคทั่วไป ได้แก่ ค่าสูงสุด เอนโทรปี เปอร์เซ็นไทล์ เป็นต้น ดังนั้น คุณจะต้องสำรวจเทคนิคเหล่านี้ นอกเหนือไปจากการทราบอัลกอริทึมการวัดเชิงปริมาณต่างๆ

ความสำคัญและความจำเป็นของการวัดปริมาณ

วัตถุประสงค์หลักของการวิเคราะห์เชิงปริมาณในเครือข่ายประสาทเทียม (NN) คือการเพิ่มความเร็วในการอนุมาน เนื่องจากปริมาณพารามิเตอร์ที่เกี่ยวข้องมีมาก การอนุมานและการฝึก NN จึงเป็นงานที่ต้องใช้การประมวลผลอย่างหนัก

ตัวอย่างเช่น NN ประกอบด้วยฟังก์ชันการเปิดใช้งาน น้ำหนัก และอคติ (เรียกอีกอย่างว่าพารามิเตอร์) และพารามิเตอร์ดังกล่าวหลายล้านรายการสามารถมีอยู่ในสถาปัตยกรรม NN เดียวได้

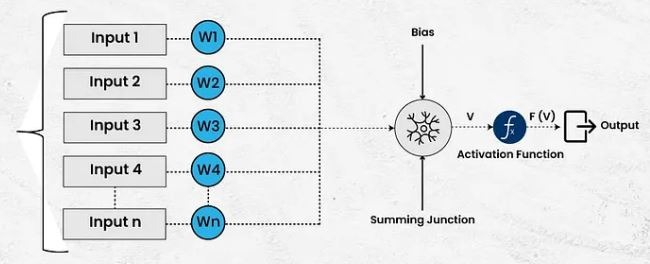
ลองพิจารณาสถาปัตยกรรม ResNet แบบ 50 เลเยอร์ แบบจำลองที่เรียบง่ายเช่นนี้จะมีน้ำหนักประมาณ 26 ล้านค่า และการเปิดใช้งาน 16 ล้านครั้ง และเมื่อจัดเก็บโดยใช้ค่าจุดลอยตัว 32 บิต จะใช้หน่วยความจำประมาณ 168 MB การดำเนินการทางคณิตศาสตร์ที่ซับซ้อนกับข้อมูลปริมาณมากเช่นนี้อาจต้องใช้ทรัพยากรอย่างมาก โดยเฉพาะอย่างยิ่งสำหรับอุปกรณ์เอจ

ด้วยการถือกำเนิดของ LLM (Large Language Models)จำนวนพารามิเตอร์จึงเพิ่มขึ้นอย่างมาก ส่งผลให้ขนาดหน่วยความจำเพิ่มขึ้นอย่างมาก เนื่องจากความสามารถในการใช้งานจริงของ NNs เพิ่มขึ้นอย่างต่อเนื่อง จึงมีความจำเป็นมากขึ้นในการนำ NNs ไปใช้ในอุปกรณ์ต่างๆ เช่น โทรศัพท์ แล็ปท็อป และสมาร์ทวอทช์ อย่างไรก็ตาม การดำเนินการ NNs ที่ซับซ้อนเช่นนี้บนอุปกรณ์เหล่านี้จะไม่สามารถทำได้หากไม่มีการวัดปริมาณ