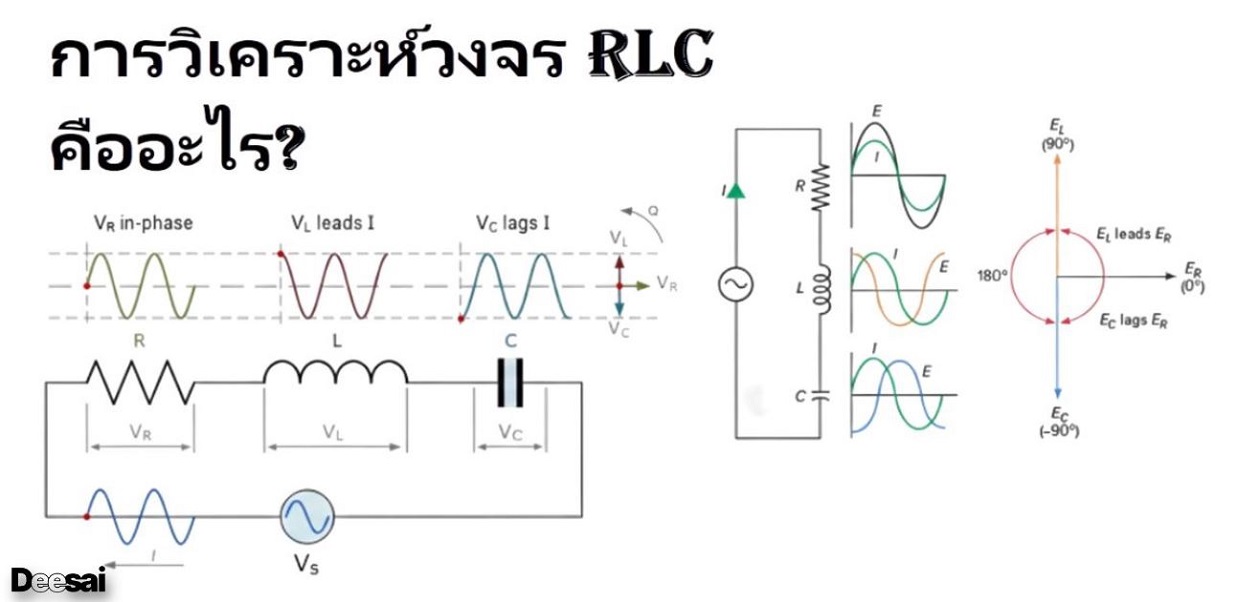
วงจร RLC ประกอบด้วยส่วนประกอบหลักสามส่วน ได้แก่ ตัวต้านทาน ตัวเหนี่ยวนํา และตัวเก็บประจุ ทั้งหมดเชื่อมต่อกับแหล่งจ่ายไฟแรงดันไฟฟ้าส่วนประกอบเหล่านี้เป็นส่วนประกอบแบบพาสซีฟ ซึ่งหมายความว่าดูดซับพลังงาน และเป็นเส้นตรง ซึ่งบ่งชี้ถึงความสัมพันธ์โดยตรงระหว่างแรงดันและกระแส

วงจร RLC สามารถเชื่อมต่อได้หลายวิธี โดยการเชื่อมต่อแบบอนุกรมและแบบขนานเป็นแบบธรรมดาที่สุดซึ่งแตกต่างจากวงจร LC ซึ่งแกว่งไปมาอย่างไม่มีกําหนด ตัวต้านทานในวงจร RLC ทําให้การสั่นสลายตัวเร็วขึ้น

วงจร RLC ซีรีส์

ในวงจร RLC แบบอนุกรมตัวต้านทานตัวเหนี่ยวนําและตัวเก็บประจุจะเชื่อมโยงกันกับแหล่งจ่ายแรงดันไฟฟ้าสร้างเส้นทางต่อเนื่องสําหรับกระแส

เนื่องจากส่วนประกอบทั้งหมดเหล่านี้เชื่อมต่อกันเป็นอนุกรมกระแสในแต่ละองค์ประกอบจึงยังคงเหมือนเดิม

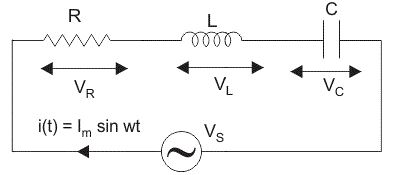
ให้ VR เป็นแรงดันไฟฟ้าข้ามตัวต้านทาน R
VL เป็นแรงดันไฟฟ้าข้ามตัวเหนี่ยวนํา L
VC เป็นแรงดันไฟฟ้าข้ามตัวเก็บประจุ C
XL เป็นรีแอกแตนซ์อุปนัย
XC เป็นรีแอกแตนซ์แบบคาปาซิทีฟ

แรงดันไฟฟ้าทั้งหมดในวงจร RLC ไม่เท่ากับผลรวมพีชคณิตของแรงดันไฟฟ้าข้ามตัวต้านทานตัวเหนี่ยวนําและตัวเก็บประจุแต่เป็นผลรวมเวกเตอร์เพราะในกรณีของตัวต้านทานแรงดันไฟฟ้าจะอยู่ในเฟสกับกระแสสําหรับตัวเหนี่ยวนําแรงดันไฟฟ้านํากระแส 90o และสําหรับตัวเก็บประจุแรงดันไฟฟ้าจะล่าช้ากว่ากระแส 90o (ตาม ELI the ICE Man)

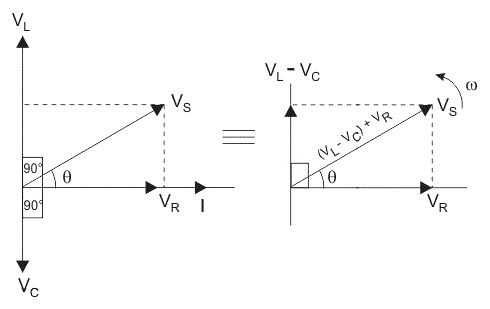
ดังนั้นแรงดันไฟฟ้าในแต่ละส่วนประกอบจึงไม่อยู่ในเฟสซึ่งกันและกันดังนั้นจึงไม่สามารถเพิ่มทางคณิตศาสตร์ได้รูปด้านล่างแสดงแผนภาพเฟสเซอร์ของวงจร RLC แบบอนุกรมสําหรับการวาดแผนภาพเฟสเซอร์สําหรับวงจรอนุกรม RLC กระแสจะถูกนํามาใช้เป็นข้อมูลอ้างอิงเนื่องจากในวงจรอนุกรมกระแสในแต่ละองค์ประกอบยังคงเท่าเดิมและเวกเตอร์แรงดันไฟฟ้าที่สอดคล้องกันสําหรับแต่ละองค์ประกอบจะถูกวาดโดยอ้างอิงถึงเวกเตอร์กระแสทั่วไป

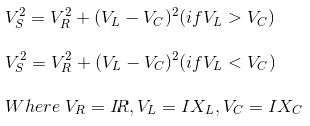
อิมพีแดนซ์สําหรับวงจร RLC แบบอนุกรม

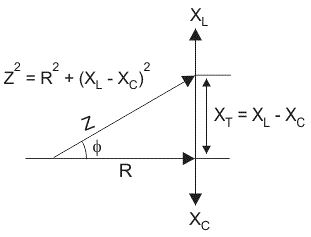
อิมพีแดนซ์ Z ของวงจร RLC แบบอนุกรมถูกกําหนดให้เป็นการต่อต้านการไหลของกระแสเนื่องจากความต้านทานวงจร R, รีแอกแตนซ์อุปนัย, XL และรีแอกแตนซ์แบบคาปาซิทีฟ,XC หากรีแอกแตนซ์อุปนัยมากกว่ารีแอกแตนซ์แบบคาปาซิทีฟเช่น XL %3EXC วงจร RLC จะมีมุมเฟสล้าหลัง และถ้ารีแอกแตนซ์แบบ capacitive มากกว่ารีแอกแตนซ์อุปนัย เช่นXC %3EXL วงจร RLC จะมีมุมเฟสนํา และถ้าทั้งอุปนัยและ capacitive เหมือนกันเช่น XL = XC วงจรจะทํางานเป็นวงจรตัวต้านทานล้วนๆ
เรารู้ว่า

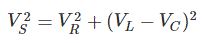
ที่ไหน

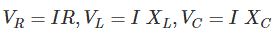
การแทนที่ค่า

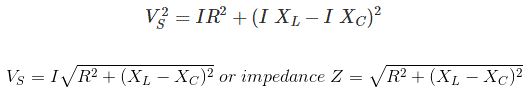
วงจร RLC แบบขนาน

ในวงจร RLC แบบขนานตัวต้านทานตัวเหนี่ยวนําและตัวเก็บประจุทั้งหมดเชื่อมต่อผ่านแหล่งจ่ายแรงดันไฟฟ้าเดียวกัน แต่ทํางานอย่างอิสระโดยมีค่าคงที่แรงดันไฟฟ้าในแต่ละตัวและกระแสรวมจะแยกระหว่างกัน

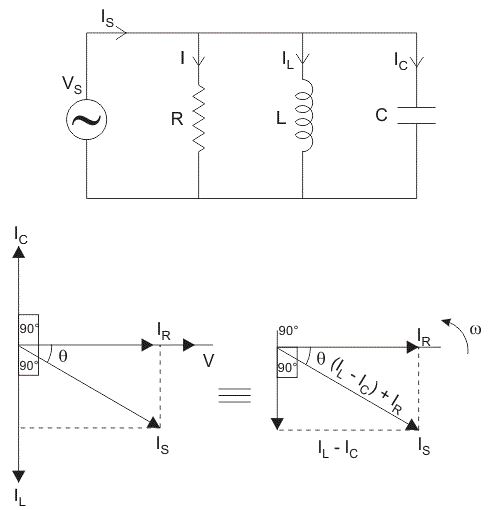
กระแสรวมที่ดึงมาจากอุปทานไม่เท่ากับผลรวมทางคณิตศาสตร์ของกระแสที่ไหลในแต่ละส่วนประกอบ แต่เท่ากับผลรวมเวกเตอร์ของกระแสทั้งหมดเนื่องจากกระแสที่ไหลในตัวต้านทานตัวเหนี่ยวนําและตัวเก็บประจุไม่ได้อยู่ในเฟสเดียวกันดังนั้นจึงไม่สามารถเพิ่มทางคณิตศาสตร์ได้

แผนภาพเฟสเซอร์ของวงจร RLC แบบขนาน IR คือกระแสที่ไหลในตัวต้านทาน R เป็นแอมป์
ICคือกระแสที่ไหลในตัวเก็บประจุ C เป็นแอมป์
IL คือกระแสที่ไหลในตัวเหนี่ยวนํา L เป็นแอมป์
ฉันคือกระแสไฟในหน่วยแอมป์
ในวงจร RLC แบบขนานส่วนประกอบทั้งหมดจะเชื่อมต่อแบบขนานดังนั้นแรงดันไฟฟ้าในแต่ละองค์ประกอบจึงเท่ากันดังนั้นสําหรับการวาดแผนภาพเฟสเซอร์ให้ใช้แรงดันไฟฟ้าเป็นเวกเตอร์อ้างอิงและกระแสอื่น ๆ ทั้งหมดเช่น IR, ICIC, IL จะถูกวาดสัมพันธ์กับเวกเตอร์แรงดันไฟฟ้านี้กระแสผ่านแต่ละองค์ประกอบสามารถพบได้โดยใช้กฎปัจจุบันของ Kirchhoff ซึ่งระบุว่าผลรวมของกระแสที่เข้าสู่ทางแยกหรือโหนดเท่ากับผลรวมของกระแสที่ออกจากโหนดนั้น

ดังที่แสดงไว้ข้างต้นในสมการของอิมพีแดนซ์ Z ของวงจร RLC แบบขนานแต่ละองค์ประกอบมีส่วนกลับของอิมพีแดนซ์ (1 / Z) เช่น การรับเข้า Y ดังนั้นในวงจร RLC แบบขนานจึงสะดวกที่จะใช้การรับเข้าแทนอิมพีแดนซ์

เสียงสะท้อนในวงจร RLC

ในวงจรที่มีตัวเหนี่ยวนําและตัวเก็บประจุพลังงานจะถูกเก็บไว้ในสองวิธีที่แตกต่างกัน

1. เมื่อกระแสไหลในตัวเหนี่ยวนําพลังงานจะถูกเก็บไว้ในสนามแม่เหล็ก
2. เมื่อมีการชาร์จตัวเก็บประจุพลังงานจะถูกเก็บไว้ในสนามไฟฟ้าสถิตย์

สนามแม่เหล็กในตัวเหนี่ยวนําถูกสร้างขึ้นโดยกระแสซึ่งได้รับจากตัวเก็บประจุที่คายประจุในทํานองเดียวกันตัวเก็บประจุจะถูกชาร์จโดยกระแสที่เกิดจากการยุบตัวของสนามแม่เหล็กของตัวเหนี่ยวนําและกระบวนการนี้ดําเนินต่อไปเรื่อย ๆ ทําให้พลังงานไฟฟ้าแกว่งระหว่างสนามแม่เหล็กและสนามไฟฟ้าในบางกรณีที่ความถี่บางอย่างที่เรียกว่าความถี่เรโซแนนซ์รีแอกแตนซ์อุปนัยของวงจรจะเท่ากับรีแอกแตนซ์แบบคาปาซิทีฟซึ่งทําให้พลังงานไฟฟ้าแกว่งระหว่างสนามไฟฟ้าของตัวเก็บประจุและสนามแม่เหล็กของตัวเหนี่ยวนําสิ่งนี้ก่อให้เกิดออสซิลเลเตอร์ฮาร์มอนิกสําหรับกระแสในวงจร RLC การมีตัวต้านทานทําให้การสั่นเหล่านี้ตายไปตามระยะเวลาหนึ่งและเรียกว่าเอฟเฟกต์การหน่วงของตัวต้านทาน

สูตรสําหรับความถี่เรโซแนนซ์

ในระหว่างการสะท้อนที่ความถี่หนึ่งเรียกว่าความถี่เรโซแนนซ์

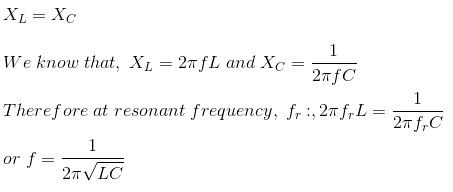
เมื่อเกิดเสียงสะท้อนปฏิกิริยาอุปนัยของวงจรจะเท่ากับรีแอกแตนซ์แบบคาปาซิทีฟซึ่งทําให้อิมพีแดนซ์ของวงจรมีค่าต่ําสุดในกรณีของวงจร RLC แบบอนุกรมแต่เมื่อตัวต้านทานตัวเหนี่ยวนําและตัวเก็บประจุเชื่อมต่อแบบขนานอิมพีแดนซ์ของวงจรจะสูงสุดดังนั้นวงจร RLC แบบขนานบางครั้งจึงเรียกว่าตัวป้องกันเรโซเนเตอร์โปรดทราบว่าความถี่เรโซแนนซ์ต่ําสุดของวัตถุที่สั่นสะเทือนเรียกว่าความถี่พื้นฐาน

ความแตกต่างระหว่างวงจร RLC แบบอนุกรมและวงจร RLC แบบขนาน

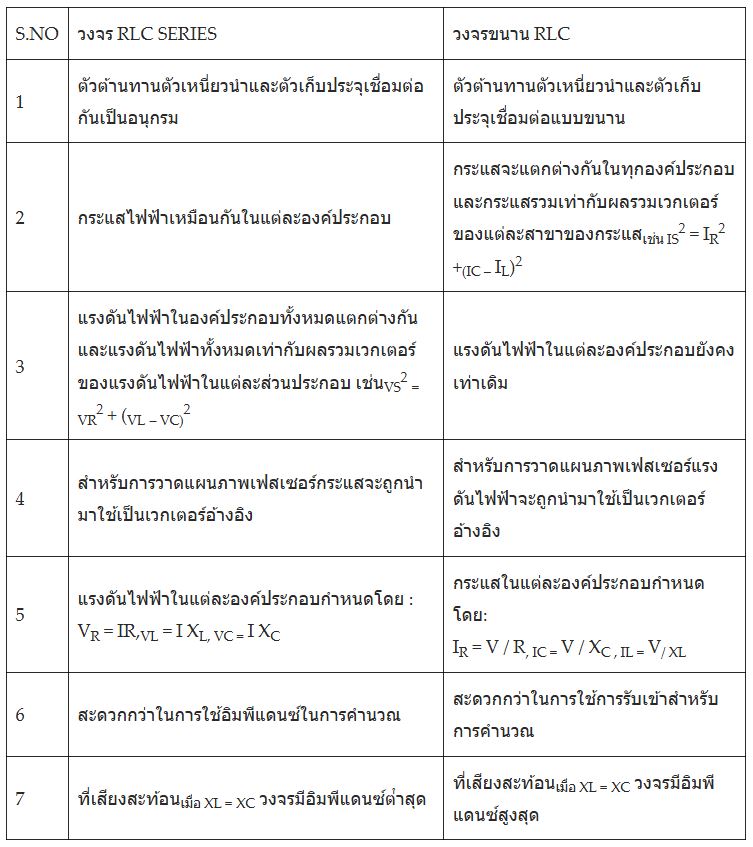
สมการของวงจร RLC

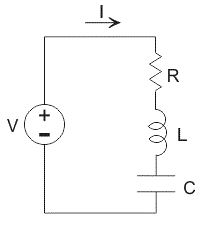
พิจารณาวงจร RLC ที่มีตัวต้านทาน R, ตัวเหนี่ยวนํา L และตัวเก็บประจุ C เชื่อมต่อกันเป็นอนุกรมและขับเคลื่อนโดยแหล่งแรงดันไฟฟ้า V ให้ Q เป็นประจุบนตัวเก็บประจุและกระแสที่ไหลในวงจรคือ I ใช้กฎแรงดันไฟฟ้าของ Kirchhoff

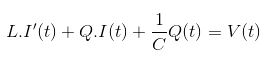
ในสมการนี้ความต้านทาน ความเหนี่ยวนํา ความจุ และแรงดันไฟฟ้าเป็นปริมาณที่ทราบ แต่กระแสและประจุเป็นปริมาณที่ไม่รู้จักเรารู้ว่ากระแสคืออัตราของประจุไฟฟ้าที่ไหล ดังนั้นจึงกําหนดโดย

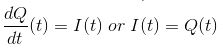
แยกความแตกต่างอีกครั้ง I'(t) = Q'' (t)

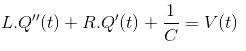
การแยกความแตกต่างของสมการข้างต้นที่เกี่ยวกับ 't' ที่เราได้รับ

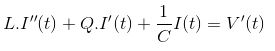
ตอนนี้ ณ เวลา t = 0, V(0) = 0 และ ณ เวลา t = t, V(t) = Eosinωt
การแยกความแตกต่างตาม 't' เราจะได้ V'(t) = ωEocosωt
แทนที่ค่าของ V'(t) ในสมการข้างต้น

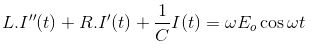
สมมติว่าคําตอบของสมการนี้คือ IP(t) = Asin(ωt – ǿ) และถ้า IP(t) เป็นคําตอบของสมการข้างต้น ก็ต้องเป็นไปตามสมการนี้

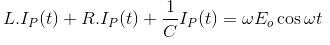
ตอนนี้แทนที่ค่าของ IP(t) และแยกความแตกต่างที่เราได้รับ

ใช้สูตรของ cos (A + B) และรวมคําศัพท์ที่คล้ายกันที่เราได้รับ

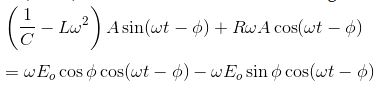
จับคู่ค่าสัมประสิทธิ์ของบาป (ωt – φ) และ cos(ωt – φ) ทั้งสองด้านที่เราได้รับ

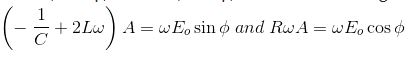
ตอนนี้เรามีสมการสองสมการและสองสมการที่ไม่รู้จัก เช่น φ และ A และโดยการหารสมการสองสมการข้างต้น

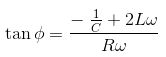
การยกกําลังสองและเพิ่มสมการข้างต้น เราจะได้

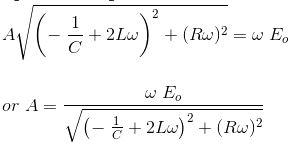
การวิเคราะห์วงจร RLC โดยใช้การแปลงลาปลาส

ขั้นตอนที่ 1 :วาดแผนภาพเฟสเซอร์สําหรับวงจรที่กําหนด
ขั้นตอนที่ 2 :ใช้กฎแรงดันไฟฟ้าของ Kirchhoff ในวงจรอนุกรม RLC และกฎปัจจุบันในวงจรขนาน RLC เพื่อสร้างสมการเชิงอนุพันธ์ในโดเมนเวลา
ขั้นตอนที่ 3 :ใช้การแปลง Laplace เพื่อแปลงสมการเชิงอนุพันธ์เหล่านี้จากโดเมนเวลาเป็นโดเมน s
ขั้นตอนที่ 4 :สําหรับการค้นหาตัวแปรที่ไม่รู้จัก ให้แก้สมการเหล่านี้
ขั้นตอนที่ 5 :ใช้การแปลง Laplace ผกผันเพื่อแปลงสมการย้อนกลับจากโดเมน s เป็นโดเมนเวลา

การประยุกต์ใช้วงจร RLC

ใช้เป็นตัวกรองความถี่ต่ํา, ตัวกรองความถี่สูง, ตัวกรองแบนด์พาส, ตัวกรองแบนด์สต็อป, ตัวคูณแรงดันไฟฟ้าและวงจรออสซิลเลเตอร์ใช้สําหรับปรับแต่งวิทยุหรือเครื่องรับสัญญาณเสียง