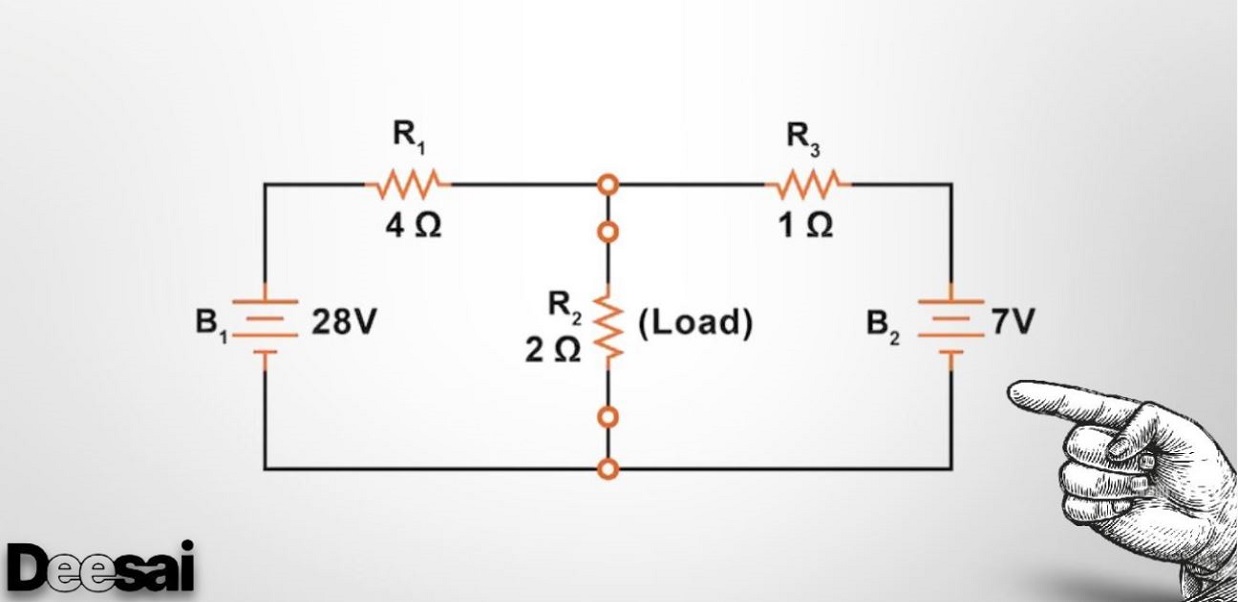
โดยทั่วไปแล้ว เราใช้กฎของโอห์มและกฎของเคอร์ชอฟฟ์เพื่อแก้ปัญหาวงจรไฟฟ้าที่ซับซ้อน แต่เราต้องตระหนักด้วยว่ามีทฤษฎีบทการวิเคราะห์วงจรมากมายที่เราสามารถคำนวณกระแสและแรงดันไฟฟ้า ณ จุดใดๆ ในวงจรได้ ในบรรดาทฤษฎีบทวงจรต่างๆ ทฤษฎีบทของเทเวนินเป็นทฤษฎีบทที่นิยมใช้มากที่สุด ในบทความนี้ เราจะมาเรียนรู้เกี่ยวกับทฤษฎีบทของเทเวนินโดยละเอียด

คำอธิบายทฤษฎีบทเทเวนิน

ทฤษฎีบทของเทเวนินระบุว่าเป็นไปได้ที่จะลดความซับซ้อนของวงจรเชิงเส้นใดๆ ก็ตาม ให้เป็นวงจรเทียบเท่าที่มีแหล่งจ่ายแรงดันไฟฟ้าตัวเดียวและความต้านทานแบบอนุกรม

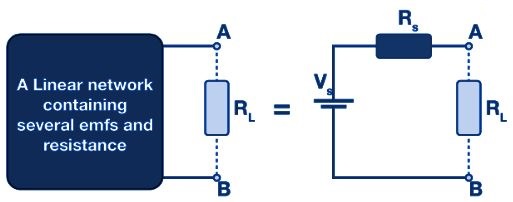
ภาพแสดงวงจรสมมูลของเทเวนิน ในภาพ เราจะเห็นว่าองค์ประกอบวงจรต้านทานหลายตัวถูกแทนที่ด้วยความต้านทานสมมูล Rs  ตัวเดียว และแหล่งพลังงานหลายแหล่งถูก แทนที่ด้วยแหล่งแรงดันไฟฟ้าสมมูล Vs

ตัวอย่างทฤษฎีบทของเทเวนิน

ให้เราทำความเข้าใจทฤษฎีบทของเทเวนินด้วยตัวอย่าง

ตัวอย่าง:

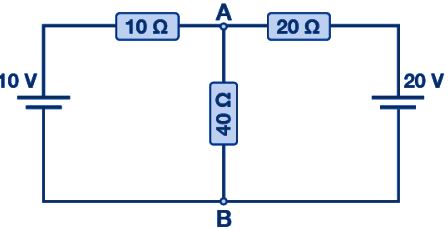
ขั้นตอนที่ 1: สำหรับการวิเคราะห์วงจรข้างต้นโดยใช้ทฤษฎีบทของ Thevenin ขั้นแรกให้ลบความต้านทานโหลดที่จุดศูนย์กลาง ในกรณีนี้คือ 40 Ω

ขั้นตอนที่ 2: กำจัดความต้านทานภายในของแหล่งจ่ายแรงดันโดยการลัดวงจรแหล่งจ่ายแรงดันทั้งหมดที่เชื่อมต่อกับวงจร กล่าวคือ v = 0 หากมีแหล่งจ่ายกระแสอยู่ในวงจร ให้กำจัดความต้านทานภายในโดยการเปิดวงจรแหล่งจ่าย ขั้นตอนนี้ทำเพื่อให้ได้แหล่งจ่ายแรงดันหรือแหล่งจ่ายกระแสที่เหมาะสมที่สุดสำหรับการวิเคราะห์

ขั้นตอนที่ 3: หาค่าความต้านทานสมมูล ในตัวอย่างนี้ ความต้านทานสมมูลของวงจรคำนวณได้ดังนี้:

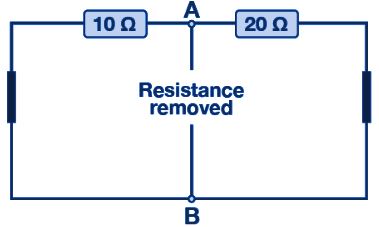
เมื่อเอาความต้านทานโหลดออกและแหล่งแรงดันไฟฟ้าลัดวงจร ความต้านทานเทียบเท่าของวงจรจะถูกคำนวณดังนี้:

ตัวต้านทาน 10 Ω ขนานกับ 20 Ω ดังนั้นความต้านทานเทียบเท่าของวงจรคือ:

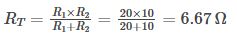
ขั้นตอนที่ 4: ค้นหาแรงดันไฟฟ้าเทียบเท่า

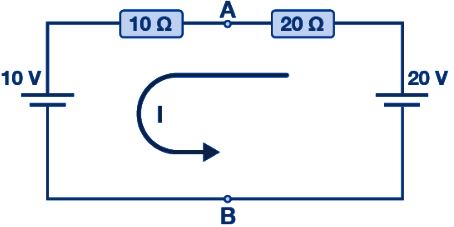
ในการคำนวณแรงดันไฟฟ้าเทียบเท่า ให้ต่อแหล่งจ่ายแรงดันไฟฟ้ากลับเข้าไปในวงจร Vs = VAB ดังนั้น กระแสที่ไหลรอบลูปจึงคำนวณได้ดังนี้

กระแสที่คำนวณได้นั้นเป็นกระแสร่วมสำหรับตัวต้านทานทั้งสองตัว ดังนั้นแรงดันตกคร่อมตัวต้านทานจึงสามารถคำนวณได้ดังนี้:

V_AB = 20 – (20 Ω x 0.33 A) = 13.33 V

หรือ,

V_AB = 10 + (10 Ω x 0.33 A) = 13.33 V

แรงดันตกคร่อมตัวต้านทานทั้งสองตัวเท่ากัน

ขั้นตอนที่ 5: วาดวงจรสมมูลของเทเวนิน วงจรสมมูลของเทเวนินประกอบด้วยความต้านทานอนุกรม 6.67 Ω และแหล่งจ่ายแรงดันไฟฟ้า 13.33 โวลต์

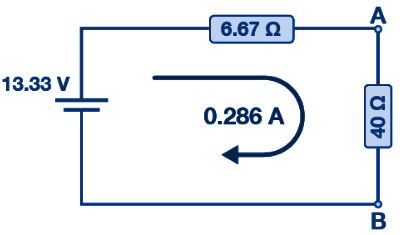
กระแสไฟฟ้าที่ไหลในวงจรคำนวณได้จากสูตรด้านล่างนี้:

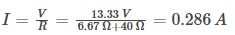
ทฤษฎีบทของเทเวนินสามารถนำไปประยุกต์ใช้กับวงจรไฟฟ้ากระแสสลับและกระแสตรงได้ แต่ควรสังเกตว่าวิธีการนี้ใช้ได้เฉพาะกับวงจรไฟฟ้ากระแสสลับที่ประกอบด้วยองค์ประกอบเชิงเส้น เช่น ตัวต้านทาน ตัวเหนี่ยวนำ และตัวเก็บประจุ เช่นเดียวกับความต้านทานสมมูลของเทเวนิน อิมพีแดนซ์สมมูลของเทเวนินได้มาจากการแทนที่แหล่งจ่ายแรงดันไฟฟ้าทั้งหมดด้วยอิมพีแดนซ์ภายในของแหล่งจ่ายแรงดันไฟฟ้าเหล่านั้น

ตัวอย่างการแก้ไขทฤษฎีบทของเทเวนิน

ค้นหา VTH , RTH และกระแสโหลด IL ที่ไหลผ่านและแรงดันไฟฟ้าโหลดข้ามตัวต้านทานโหลดในวงจรด้านล่างโดยใช้ทฤษฎีบทของ Thevenin

สารละลาย:

ขั้นตอนที่ 1: ถอด 5 kΩ ออกจากวงจร

ขั้นตอนที่ 2: วัดแรงดันไฟฟ้าวงจรเปิด คุณจะได้ค่าแรงดันไฟฟ้าเทเวนิน (V_TH)

ขั้นตอนที่ 3: เราคำนวณแรงดันไฟฟ้าของ Thevenin โดยการกำหนดกระแสที่ไหลผ่านตัวต้านทาน 12 kΩ และ 4 kΩ

เนื่องจากตัวต้านทานทั้งสองตัวเชื่อมต่อแบบอนุกรม จึงสามารถคำนวณกระแสที่ไหลผ่านตัวต้านทานได้ดังนี้:

I = 48 V /( 12 kΩ + 4 kΩ) = 3 mA

สามารถคำนวณแรงดันไฟฟ้าข้ามตัวต้านทาน 4 kΩ ได้ดังนี้:

3 mA x 4 kΩ = 12 V

เนื่องจากไม่มีกระแสไหลผ่านตัวต้านทาน 8 kΩ จึงไม่เกิดแรงดันตกคร่อมตัวต้านทาน ดังนั้นแรงดันคร่อมขั้ว AB จึงเท่ากับแรงดันคร่อมตัวต้านทาน 4 kΩ ดังนั้น แรงดัน 12 V จะปรากฏที่ขั้ว AB ดังนั้น แรงดันเทเวนิน V_TH = 12 V

ขั้นตอนที่ 4: ลัดวงจรแหล่งจ่ายแรงดันไฟฟ้าดังแสดงในรูปด้านล่าง:

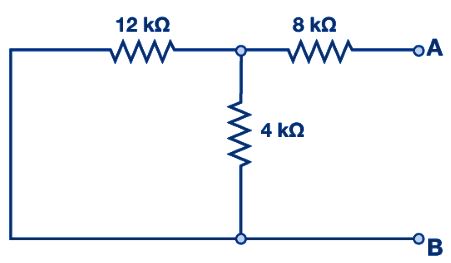
ขั้นตอนที่ 5: คำนวณความต้านทานของเทเวนิน

โดยการวัดความต้านทานวงจรเปิด เราสามารถวัดความต้านทานของเทเวนินได้

เราสังเกตว่าตัวต้านทาน 8 kΩ ต่ออนุกรมกับตัวต้านทาน 12 kΩ และ 4 kΩ แบบขนาน ดังนั้น ความต้านทานเทียบเท่าหรือความต้านทานของเทเวนินจึงคำนวณได้ดังนี้

8kΩ + (4kΩ || 12kΩ)

R_TH = 8 kΩ + [(4 kΩ x 12 kΩ) / (4 kΩ + 12 kΩ)]

R_TH = 8kΩ + 3kΩ

R_TH = 11 kΩ

ขั้นตอนที่ 6: ตอนนี้เชื่อมต่อ RTH แบบอนุกรมกับแหล่งจ่ายแรงดัน VTH และตัวต้านทานโหลดตามที่แสดงในภาพ

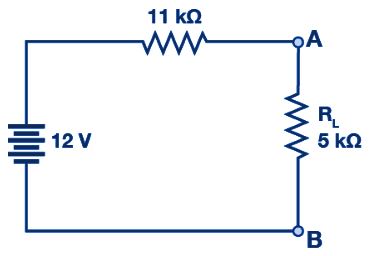
ขั้นตอนที่ 7: สำหรับขั้นตอนสุดท้าย ให้คำนวณแรงดันโหลดและกระแสโหลดโดยใช้กฎของโอห์มดังนี้:

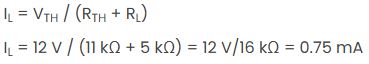
แรงดันโหลดจะถูกกำหนดดังต่อไปนี้:

V_L = 0.75 mA x 5 kΩ = 3.75 V

การประยุกต์ใช้ทฤษฎีบทเทเวนิน

• ทฤษฎีบทของเทเวนินใช้ในการวิเคราะห์ระบบไฟฟ้า
• ทฤษฎีบทของเทเวนินใช้ในการสร้างแบบจำลองแหล่งกำเนิดและการวัดความต้านทานโดยใช้สะพานวีทสโตน

ข้อจำกัดของทฤษฎีบทเทเวนิน

• ทฤษฎีบทของเทเวนินใช้เฉพาะในการวิเคราะห์วงจรเชิงเส้นเท่านั้น
• การสูญเสียพลังงานของค่าเทียบเท่า Thevenin ไม่เหมือนกับการสูญเสียพลังงานของระบบจริง

คำถามที่พบบ่อย – FAQ

ทฤษฎีบทเทเวนินคืออะไร?

ทฤษฎีบทของเทเวนินระบุว่าเป็นไปได้ที่จะลดความซับซ้อนของวงจรเชิงเส้นใดๆ ก็ตาม ให้เป็นวงจรเทียบเท่าที่มีแหล่งจ่ายแรงดันไฟฟ้าตัวเดียวและความต้านทานแบบอนุกรม

Thevenin Voltage คืออะไร?

- แรงดันไฟฟ้าวงจรเปิดที่ปรากฏข้ามขั้วทั้งสองคือแรงดันไฟฟ้า Thevenin

ทฤษฎีบทของเทเวนินใช้ที่ไหน

- ทฤษฎีบทของเทเวนินใช้ในการวิเคราะห์ระบบไฟฟ้า

ทฤษฎีบทของเทเวนินสามารถนำไปใช้กับวงจรที่ไม่เป็นเชิงเส้นได้หรือไม่

- ไม่ ทฤษฎีบทของ Thevenin ไม่สามารถนำไปใช้กับวงจรที่ไม่เป็นเชิงเส้นได้

ทฤษฎีบทของเทเวนินสามารถนำไปใช้กับวงจรไฟฟ้ากระแสสลับได้หรือไม่?

- ใช่ ทฤษฎีบทของ Thevenin นำไปใช้กับวงจรไฟฟ้ากระแสสลับได้