K-maps พร้อมตัวแปรที่ป้อน

แผนที่ตัวแปรที่เข้ามาทำให้กระบวนการง่ายขึ้นอีกขั้นด้วยการย่อขนาดแผนที่ K ให้เล็กลง การบีบอัดแผนที่ทำให้เห็นภาพและลดขนาดระบบหลายตัวแปรได้ง่ายขึ้นมาก

ตารางความจริงเป็นกลไกที่ดีที่สุดในการระบุพฤติกรรมของวงจรลอจิกเชิงผสมที่กำหนดอย่างสมบูรณ์ และ K-map เป็นกลไกที่ดีที่สุดในการแสดงภาพและลดความสัมพันธ์ระหว่างอินพุตและเอาต์พุตของวงจรลอจิกดิจิทัล จนถึงตอนนี้ เราได้แสดงตัวแปรอินพุตที่ด้านบนซ้ายของตารางความจริงและรอบขอบของ K-map ซึ่งทำให้ทุกสถานะของสัญญาณเอาต์พุตถูกกำหนดเป็นฟังก์ชันของรูปแบบอินพุตของ 0 และ 1 ในแถวที่กำหนดในตารางความจริง หรือเป็นรหัสไบนารีสำหรับเซลล์ K-map ที่กำหนด ตารางความจริงและ K-map สามารถแปลงให้อยู่ในรูปแบบที่กระชับมากขึ้นได้โดยไม่สูญเสียข้อมูลใดๆ โดยการย้ายตัวแปรอินพุตจากด้านบนซ้ายของตารางความจริงไปยังคอลัมน์เอาต์พุต หรือจากภายนอก K-map ไปยังภายในเซลล์ของ K-map แม้ว่าจะยังไม่ชัดเจนจนกว่าจะถึงโมดูลถัดไป การใช้ ตัวแปรที่ป้อนเข้า  ตารางความจริงแบบบีบอัด และ K-map มักจะทำให้ระบบหลายตัวแปรมองเห็นและลดขนาดได้ง่ายขึ้นมาก

กลไกการแปลแสดงไว้ในภาพด้านล่าง ซึ่งตารางความจริง 16 แถวถูกบีบอัดให้เป็นตารางความจริงทั้ง 8 แถวและ 4 แถว ในตารางความจริง 8 แถว ตัวแปร D จะไม่ถูกใช้เพื่อระบุคอลัมน์อินพุตอีกต่อไป แต่จะปรากฏในคอลัมน์เอาต์พุต ซึ่งเข้ารหัสความสัมพันธ์ระหว่างค่าลอจิกเอาต์พุตสองแถวและอินพุต D ในตารางความจริง 4 แถว ตัวแปร C และ D จะไม่ถูกใช้เพื่อระบุคอลัมน์อินพุตอีกต่อไป แต่จะอยู่ในคอลัมน์เอาต์พุต ซึ่งเข้ารหัสความสัมพันธ์ระหว่างค่าลอจิกเอาต์พุตสี่แถวและอินพุต C และ D

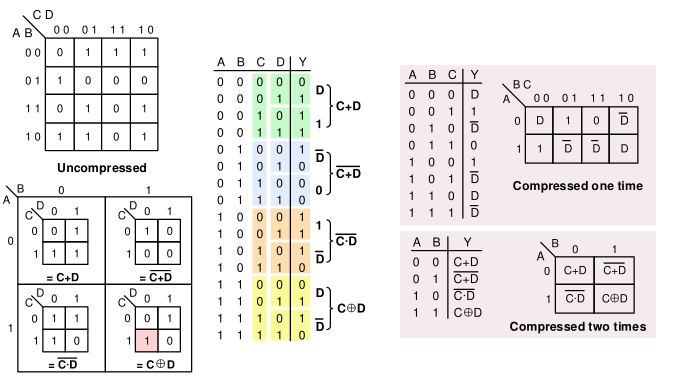
แผนที่ K-map แบบ 4 เซลล์ถูกแสดงทางด้านขวา โดยในครั้งนี้จะแสดงแผนที่ย่อยที่แสดงความสัมพันธ์ระหว่าง C และ D สำหรับค่าเฉพาะสี่ค่าของตัวแปร A และ B สำหรับตัวแปร K-map ใดๆ ที่ป้อนเข้ามา การคิด (หรือการร่างภาพ) แผนที่ย่อยสามารถช่วยระบุการเข้ารหัสที่ถูกต้องสำหรับตัวแปรที่ป้อนเข้ามาได้ โปรดทราบว่าหมายเลขแถวของตารางความจริงสามารถแมปไปยังเซลล์ในแผนที่ย่อยได้โดยการอ่านรหัสดัชนี K-map เริ่มต้นด้วยรหัส super-map และผนวกรหัสแผนที่ย่อย ตัวอย่างเช่น กล่องแรเงาในแผนที่ย่อยอยู่ในกล่องหมายเลข 1110

การบีบอัดแผนที่แบบเดียวกันนี้แสดงไว้ด้านล่าง โดยแสดงการแมปจาก K-map ที่ไม่ได้บีบอัดไปยัง K-map ที่ถูกบีบอัดโดยตรง สีแสดงวิธีการแปลงเซลล์ในแผนที่ที่ไม่ได้บีบอัดไปยังเซลล์ในแผนที่ที่ถูกบีบอัด โปรดทราบว่าเซลล์สองเซลล์ในแผนที่ 16 เซลล์ถูกบีบอัดเป็นเซลล์เดียวในแผนที่ 8 เซลล์ และเซลล์สี่เซลล์ในแผนที่ 16 เซลล์ถูกบีบอัดเป็นเซลล์เดียวในแผนที่ 4 เซลล์

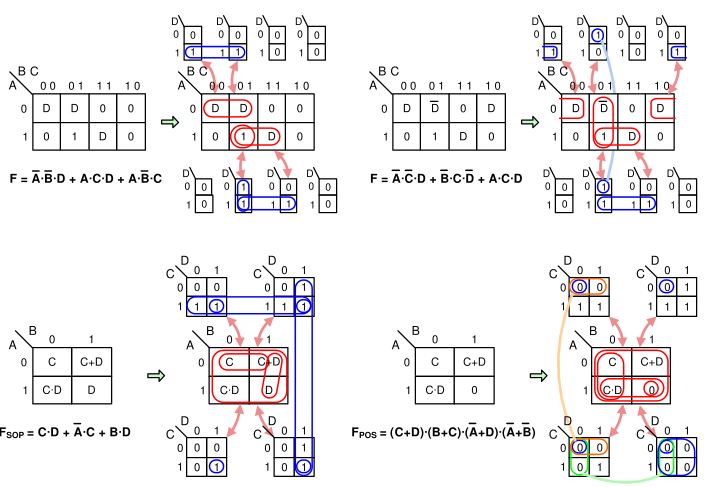
สมการ SOP ของ Minterm และสมการ POS ของ Maxterm สามารถแปลงเป็นตัวแปร K-map ที่ป้อนเข้าได้โดยตรง ดังแสดงในภาพประกอบด้านล่าง (ตัวเลขที่เล็กกว่าที่ด้านล่างของเซลล์ K-map แสดงหมายเลขของ Minterm หรือ Maxterm ที่กำหนดให้กับเซลล์นั้น) เมื่อเข้ารหัส Minterm หรือ Maxterm ลงใน K-map จะใช้จำนวนตัวแปรอินพุตน้อยที่สุด ตัวอย่างเช่น หาก Minterm ที่ใหญ่ที่สุดคือ 14 ตัว จะถือว่ามีตัวแปรอินพุตสี่ตัว

การวนซ้ำตัวแปร K-maps ที่ป้อนเข้ามานั้นเป็นไปตามหลักการทั่วไปเช่นเดียวกับการวนซ้ำ '1-0' map นั่นคือ การหากลุ่มที่เหมาะสมที่สุดของ 1 และตัวแปรที่ป้อนเข้ามา (EV) จะถูกค้นหาสำหรับวงจร SOP และการหากลุ่มที่เหมาะสมที่สุดของ 0 และ EV จะถูกค้นหาสำหรับวงจร POS กฎเกณฑ์มีความคล้ายคลึงกัน คือ EV ทั้งหมดและ 1 (หรือ 0) ทั้งหมดต้องถูกจัดกลุ่มให้อยู่ในกลุ่มสี่เหลี่ยมหรือสี่เหลี่ยมจัตุรัสที่มีขนาด "ยกกำลัง 2" มากที่สุดเท่าที่จะเป็นไปได้ และกระบวนการจะเสร็จสมบูรณ์เมื่อ EV ทั้งหมดและ 1 (หรือ 0) ทั้งหมดถูกรวมไว้ในลูปที่เหมาะสมที่สุด ข้อแตกต่างคือ EV ที่คล้ายกันสามารถรวมอยู่ในลูปเดี่ยวๆ หรือรวมกับ 1 (หรือ 0) ได้ และต้องใช้ความระมัดระวังเมื่อวนลูปเซลล์ด้วย 1 (หรือ 0) เนื่องจาก '1' (หรือ '0') บ่งชี้ว่า EV ที่เป็นไปได้ทั้งหมดอยู่ในเซลล์แผนที่นั้น และลูปที่รวม 1 (หรือ 0) เข้ากับ EV มักจะรวมเฉพาะเซตย่อยของ EV ที่เป็นไปได้ทั้งหมดเท่านั้น (แสดงในรูปที่ 4 ด้านล่าง) การวนลูป EV K-map จะเสร็จสมบูรณ์เมื่อ minterms หรือ maxterms ทั้งหมดอยู่ในกลุ่มที่เหมาะสม บางทีสิ่งที่ท้าทายที่สุดคือการตรวจสอบให้แน่ใจว่า EV ที่เป็นไปได้ทั้งหมดถูกนำมาพิจารณาในเซลล์ที่มี 1 (หรือ 0)

เพื่อช่วยให้เข้าใจการวนซ้ำใน EV K-map อาจเป็นประโยชน์หากลองนึกถึงซับแมปที่เซลล์ K-map ทุกเซลล์มีนัยแฝงอยู่ ดังที่แสดงในรูปด้านล่าง ตัวแปรในเซลล์ K-map สามารถเกิดขึ้นได้จากการวนซ้ำข้อมูล '1-0' ที่ป้อนลงในเซลล์ในซับแมปที่นัยแฝงอยู่ การวนซ้ำข้อมูลในเซลล์ที่อยู่ติดกันใน EV K-map สามารถรวมค่า 1 (หรือ 0) ในซับแมปที่ปรากฏในตำแหน่งเดียวกันในซับแมปได้

เมื่ออ่านสมการลูป พจน์ผลคูณ SOP (หรือพจน์ผลรวม POS) ของแต่ละลูปต้องประกอบด้วยตัวแปรที่กำหนดโดเมนลูปและค่า EV ที่มีอยู่ในลูป ตัวอย่างเช่น ในตัวอย่างแรกด้านล่าง พจน์ SOP แรก ABD ประกอบด้วยโดเมนลูป AB และตัวแปร D ที่ป้อนเข้าไป

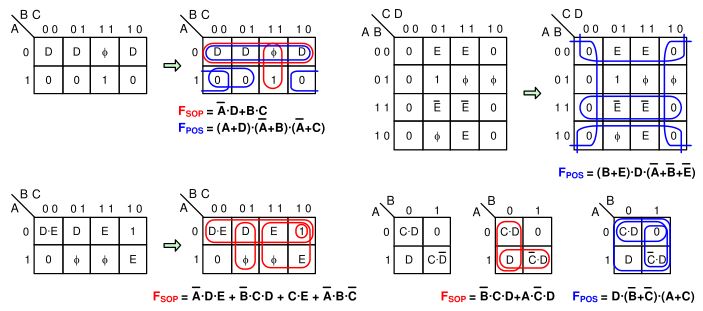
เซลล์ในแผนที่ตัวแปรที่ป้อนอาจมีตัวแปรที่ป้อนเพียงตัวเดียวหรือนิพจน์ตรรกะของตัวแปรสองตัวหรือมากกว่า เมื่อวนซ้ำเซลล์ที่มีนิพจน์ตรรกะ จะช่วยให้เข้าใจถึงความแตกต่างในกลไกการวนซ้ำของ SOP และ POS เมื่อเปรียบเทียบกับ EV ตัวเดียวในเซลล์ K-map เทอมผลคูณในเซลล์จะแสดงโดเมน SOP ที่เล็กกว่า เนื่องจากยิ่งตัวแปรในเทอมผลคูณมีตัวแปร AND มากเท่าใด โดเมนตรรกะที่กำหนดก็จะเล็กลงเท่านั้น เทอมผลรวมในเซลล์จะแสดงโดเมน SOP ที่ใหญ่กว่า เนื่องจากยิ่งตัวแปรในเทอมผลคูณมีตัวแปร OR มากเท่าใด โดเมนตรรกะที่กำหนดก็จะใหญ่ขึ้นเท่านั้น เมื่อวนซ้ำสมการ SOP จากแผนที่ EV เซลล์ที่มีเทอมผลคูณจะมี 1 ในแผนที่ย่อยน้อยกว่าเซลล์ที่มี EV เดี่ยว และเซลล์ที่มีเทอมผลคูณจะมี 1 มากกว่า ในทำนองเดียวกัน เมื่อวนซ้ำสมการ POS จากแผนที่ EV เซลล์ที่มีเทอมผลคูณจะมี 0 ในแผนที่ย่อยน้อยกว่าเซลล์ที่มี EV เดี่ยว และเซลล์ที่มีเทอมผลคูณจะมี 0 มากกว่า

ตัวแปร Don't care ใน K-map ที่ป้อนเข้ามานั้นมีวัตถุประสงค์เดียวกันกับที่ใช้ใน K-map '1-0' นั่นคือ ระบุเงื่อนไขอินพุตที่ไม่สามารถเกิดขึ้นได้หรือไม่เกี่ยวข้อง และสามารถจัดกลุ่มตัวแปร 1, 0 หรือตัวแปรที่ป้อนเข้ามาได้ตามต้องการเพื่อลดความยุ่งยากทางตรรกะ ดังแสดงในรูปที่ 5 ด้านล่าง ตัวแปร Don't care ที่กำหนดสามารถถูกมองว่าเป็นตัวแปร '1', '0' หรือตัวแปรที่ป้อนเข้ามาได้ตามต้องการสำหรับลูปใดๆ

ความคิดที่สำคัญ

• ตารางความจริงและ K-map สามารถแปลให้อยู่ในรูปแบบที่กระชับมากขึ้นได้โดยไม่สูญเสียข้อมูลใดๆ โดยการย้ายตัวแปรอินพุตจากด้านบนซ้ายของตารางความจริงไปยังคอลัมน์เอาต์พุต หรือจากภายนอก K-map ไปยังภายในเซลล์ของ K-map
• สมการ SOP ของ Minterm และสมการ POS ของ maxterm สามารถแปลเป็นตัวแปร K-map ที่ป้อนเข้าไปโดยตรงได้เช่นกัน
• การวนซ้ำตัวแปร K-maps ที่ป้อนจะปฏิบัติตามหลักการทั่วไปเดียวกันกับการวนซ้ำแผนที่ '1-0'
• เซลล์ในแผนที่ตัวแปรที่ป้อนอาจมีตัวแปรที่ป้อนเพียงตัวเดียวหรือนิพจน์ตรรกะของตัวแปรสองตัวหรือมากกว่า
• ไม่สนใจว่าตัวแปรที่ป้อนเข้ามา K-maps จะมีวัตถุประสงค์เดียวกันกับที่ใช้ในแผนที่ '1-0'