ทฤษฎีบทของนอร์ตันมีความคล้ายคลึงกับ ทฤษฎีบทของเทเวนิน ตรงที่ช่วยให้เราลดความซับซ้อนของวงจรเชิงเส้นใดๆ ให้เป็นวงจรสมมูลได้ อย่างไรก็ตาม แทนที่จะใช้ แหล่งจ่ายแรงดันไฟฟ้า และความต้านทานแบบอนุกรม วงจรสมมูลของนอร์ตันจะประกอบด้วย แหล่งจ่ายกระแสไฟฟ้า ที่มีความต้านทานแบบขนาน การใช้ทฤษฎีบทของนอร์ตันเพื่อลดความซับซ้อนของเครือข่ายสามารถทำให้การประเมินโหลดที่แปรผันง่ายขึ้นมาก

การนำทฤษฎีบทของนอร์ตันมาใช้กับวงจรเชิงเส้น

ทฤษฎีบทของนอร์ตันถูกจำกัดให้ใช้กับวงจรเชิงเส้นเช่นเดียวกับทฤษฎีบทของเทเวนินและทฤษฎีบทซ้อนทับ โดยที่สมการพื้นฐานทั้งหมดไม่มีเลขชี้กำลังหรือราก วงจรจะเป็นเชิงเส้นก็ต่อเมื่อใช้เฉพาะ ส่วนประกอบแบบพาสซีฟมาตรฐาน เช่น ตัว ต้านทานตัวเหนี่ยวนำและ ตัวเก็บประจุนอกจากนี้ แหล่งจ่ายแรงดันไฟฟ้า แบตเตอรี่ และแหล่งจ่ายกระแสไฟฟ้าส่วนใหญ่ยังเป็นแบบเชิงเส้นอีกด้วย

เริ่มต้นด้วยการอธิบายทฤษฎีบทของนอร์ตันโดยใช้วงจรตัวอย่างเดียวกัน (รูปที่ 1) ที่เราใช้อธิบาย วิธีการวิเคราะห์เครือข่าย อื่นๆ ของเรา เช่น:

• สาขาปัจจุบัน
• กระแสตาข่าย
• ทฤษฎีบทซ้อนทับ
• ทฤษฎีบทของเทเวนิน
• ทฤษฎีบทของมิลแมน

วิธีนี้จะทำให้คุณเปรียบเทียบวิธีการต่างๆ ได้ง่ายยิ่งขึ้น

รูปที่ 1 แผนผังวงจรสำหรับการอธิบายทฤษฎีบทของนอร์ตัน

วงจรเทียบเท่านอร์ตันคืออะไร?

ทฤษฎีบทของนอร์ตันทำให้เราสามารถลบความต้านทานโหลดออกจากวงจรเดิมในรูปที่ 1 ได้ชั่วคราว และลดสิ่งที่เหลือให้เหลือเพียงวงจรเทียบเท่าที่ประกอบด้วยแหล่งกระแสไฟฟ้าตัวเดียวและความต้านทานแบบขนาน

จากนั้นสามารถเชื่อมต่อความต้านทานโหลดเข้ากับวงจรเทียบเท่าของ Norton อีกครั้งเพื่อให้สามารถคำนวณได้ราวกับว่าเครือข่ายทั้งหมดเป็น วงจรขนานธรรมดา

หลังจากการแปลงนอร์ตัน วงจรในรูปที่ 1 ของเราจะลดลงเหลือวงจรเทียบเท่านอร์ตันในรูปที่ 2

รูปที่ 2 วงจรเทียบเท่านอร์ตันที่มีตัวต้านทานโหลด

จำไว้ว่าแหล่งจ่ายกระแสไฟฟ้าคือส่วนประกอบที่มีหน้าที่จ่ายกระแสไฟฟ้าในปริมาณคงที่ โดยจ่ายแรงดันไฟฟ้ามากหรือน้อยตามความจำเป็นเพื่อรักษากระแสไฟฟ้าคงที่นั้น

การคำนวณวงจรเทียบเท่านอร์ตัน—กระแสนอร์ตันและความต้านทานนอร์ตัน

เช่นเดียวกับทฤษฎีบทของเทเวนิน ทุกอย่างในวงจรเดิมยกเว้นความต้านทานโหลดได้รับการลดขนาดลงเป็นวงจรเทียบเท่าที่วิเคราะห์ได้ง่ายกว่า เช่นเดียวกับทฤษฎีบทของเทเวนิน ขั้นตอนที่ใช้ในทฤษฎีบทของนอร์ตันเพื่อคำนวณกระแสแหล่งที่มาของนอร์ตัน (INorton) และความต้านทานของนอร์ตัน (RNorton) โดยทั่วไปจะคล้ายคลึงกัน

ขั้นตอนที่ 1: ถอดตัวต้านทานโหลดออก

ขั้นตอนแรกคือการระบุความต้านทานโหลดและลบออกจากวงจรเดิมตามที่แสดงในรูปที่ 3

รูปที่ 3. ถอดตัวต้านทานโหลดออก

ขั้นตอนที่ 2: คำนวณค่ากระแสนอร์ตัน

ในการค้นหากระแสนอร์ตัน (สำหรับแหล่งกระแสในวงจรเทียบเท่านอร์ตัน) ให้วางการเชื่อมต่อสายตรง (ไฟฟ้าลัดวงจร) ระหว่างจุดโหลดและระบุกระแสผลลัพธ์ (รูปที่ 4)

รูปที่ 4 คำนวณกระแสไฟฟ้านอร์ตัน

โปรดทราบว่าขั้นตอนนี้ตรงข้ามกับขั้นตอนในทฤษฎีบทของ Thevenin ซึ่งเราได้แทนที่ตัวต้านทานโหลดด้วยเบรกเกอร์ (วงจรเปิด) และคำนวณแรงดันไฟฟ้า

การคำนวณปัจจุบันค่อนข้างตรงไปตรงมาสำหรับวงจรของรูป เนื่องจากโหนดระหว่าง R1 และ R3 ถูกลัดวงจรไปยังขั้วลบของแบตเตอรี่ทั้งสองก้อน โดยใช้ กฎกระแสของ Kirchhoff (KCL)เราทราบว่า:

ตอนนี้ใช้ กฎของโอห์ม กับกระแสของสาขาแต่ละสาขา:

เราสามารถแก้หาค่ากระแสไฟฟ้าลัดวงจรได้:

ขั้นตอนที่ 3: เปลี่ยนแหล่งพลังงาน

เพื่อหาค่าความต้านทานนอร์ตันสำหรับวงจรเทียบเท่าของเรา ขณะนี้เราสามารถเปลี่ยนแหล่งจ่ายไฟจากวงจรในรูปที่ 3 ได้ ดังที่แสดงในรูปที่ 5

รูปที่ 5. เปลี่ยนแหล่งจ่ายไฟในวงจร

แหล่งจ่ายแรงดันไฟฟ้าจะถูกแทนที่ด้วยวงจรไฟฟ้าลัดวงจร และแหล่งจ่ายกระแสไฟฟ้าจะถูกแทนที่ด้วยวงจรเปิด กระบวนการเปลี่ยนแหล่งจ่ายไฟนี้เหมือนกันกับที่ใช้สำหรับทฤษฎีบทซูเปอร์โพซิชันและทฤษฎีบทของเทเวนิน

ขั้นตอนที่ 4: คำนวณค่าความต้านทานนอร์ตัน

หลังจากเปลี่ยนแหล่งจ่ายแรงดันไฟฟ้าทั้งสองแหล่งแล้ว ความต้านทานรวมที่วัดได้ที่ตำแหน่งของโหลดที่ถอดออกจะเท่ากับ R1 และ R3 แบบขนาน ดังที่แสดงในรูปที่ 6

รูปที่ 6 คำนวณค่าความต้านทานนอร์ตัน

ค่าความต้านทานเทียบเท่านอร์ตันคำนวณได้ดังนี้:

ค่า 0.8 Ω นี้คือค่าความต้านทานนอร์ตัน (RNorton) ของเรา

ขั้นตอนที่ 5: วาดวงจรเทียบเท่านอร์ตัน

ขณะนี้สามารถใช้วงจรเทียบเท่า Norton แบบง่ายที่แสดงในรูปที่ 7 สำหรับการคำนวณอุปกรณ์โหลดเชิงเส้นใดๆ ที่เชื่อมต่อระหว่างจุดเชื่อมต่อได้

รูปที่ 7. วาดวงจรเทียบเท่าของนอร์ตัน

ในรูปนี้ เราได้ต่อตัวต้านทานโหลด 2 Ω จากวงจรเดิมกลับเข้าที่

การใช้วงจรเทียบเท่านอร์ตัน

หลังจากทำตามขั้นตอนทั้งหมดแล้ว ต่อไปเราจะวิเคราะห์วงจร Norton ตามที่แสดงในรูปที่ 7 เพื่อกำหนดกระแสผ่านตัวต้านทานโหลดและ แรงดันตกคร่อม ตัวต้านทาน ซึ่งตอนนี้เป็นเพียงตัวต้านทานสองตัวที่ขนานกัน ดังนั้นเราสามารถกำหนดความต้านทานรวมที่แหล่งจ่ายกระแส Norton มองเห็นได้ดังนี้:

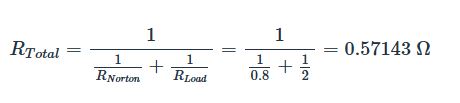
โดยใช้ วิธีตารางเราสามารถแทนค่าความต้านทานรวมลงในตาราง 1 จากนั้นกรอกส่วนที่เหลือของตาราง ตัวต้านทานโหลดมีกระแส 4.0 A และแรงดันตก 8 V

ตารางที่ 1 การคำนวณกระแสโหลดและแรงดันตก

เช่นเดียวกับวงจรเทียบเท่า Thevenin ข้อมูลที่เป็นประโยชน์เพียงอย่างเดียวจากการวิเคราะห์นี้คือค่าแรงดันไฟและกระแสไฟฟ้าสำหรับตัวต้านทานโหลด R2 ของเรา ข้อมูลที่เหลือไม่เกี่ยวข้องกับวงจรเดิม

อย่างไรก็ตาม ข้อดีเดียวกันที่พบในทฤษฎีบทของเทเวนินนั้นสามารถนำไปใช้กับทฤษฎีบทของนอร์ตันได้เช่นกัน กล่าวคือ หากเราต้องการวิเคราะห์แรงดันไฟและกระแสไฟฟ้าของตัวต้านทานโหลดในค่าความต้านทานโหลดที่แตกต่างกันหลายค่า เราสามารถใช้วงจรเทียบเท่าของนอร์ตันซ้ำแล้วซ้ำเล่า โดยไม่ต้องใช้อะไรที่ซับซ้อนกว่าการวิเคราะห์วงจรขนานธรรมดาเพื่อพิจารณาว่าเกิดอะไรขึ้นกับโหลดทดลองแต่ละค่า

ทบทวนทฤษฎีบทของนอร์ตันและวงจรเทียบเท่าของนอร์ตัน

ทฤษฎีบทของนอร์ตันระบุว่าวงจรเชิงเส้นทั้งหมดสามารถลดความซับซ้อนให้เหลือวงจรเทียบเท่าที่มีแหล่งจ่ายกระแสไฟฟ้าตัวเดียวขนานกับตัวต้านทานตัวเดียวที่เชื่อมต่อกับโหลด

• ขั้นตอนที่ 1: ถอดตัวต้านทานโหลดออกและเปลี่ยนด้วยไฟฟ้าลัดวงจร
• ขั้นตอนที่ 2: คำนวณกระแสนอร์ตัน—กระแสไฟฟ้าผ่านไฟฟ้าลัดวงจร
• ขั้นตอนที่ 3: เปลี่ยนแหล่งจ่ายไฟ แหล่งจ่ายแรงดันไฟฟ้าทั้งหมดจะถูกแทนที่ด้วยวงจรไฟฟ้าลัดวงจร และแหล่งจ่ายกระแสไฟฟ้าทั้งหมดจะถูกแทนที่ด้วยวงจรเปิด
• ขั้นตอนที่ 4: คำนวณค่าความต้านทานนอร์ตัน ซึ่งเป็นค่าความต้านทานรวมระหว่างจุดเชื่อมต่อวงจรเปิดหลังจากถอดแหล่งกำเนิดทั้งหมดออกแล้ว
• ขั้นตอนที่ 5: วาดวงจรเทียบเท่า Norton โดยให้แหล่งกระแส Norton ขนานกับความต้านทาน Norton ตัวต้านทานโหลดจะต่อกลับระหว่างจุดเปิดสองจุดของวงจรเทียบเท่า
• วิเคราะห์แรงดันและกระแสไฟฟ้าสำหรับโหลดตามกฎของวงจรขนาน